题目内容
已知复数:z1=log2(2x+1)+ki,z2=1-xi(其中x,k∈R),记f(x)=Re(1)试写出f(x)关于x的函数解析式
(2)若函数f(x)是偶函数,求k的值
(3)求证:对任意实数m,由(2)所得函数y=f(x)的图象与直线y=
 x+m的图象最多只有一个交点.
x+m的图象最多只有一个交点.
【答案】分析:(1)由z1=log2(2x+1)+ki,z2=1-xi,求出z1•z2后,结合f(x)=Re(z1•z2),可得f(x)关于x的函数解析式
(2)根据函数f(x)是偶函数,根据偶函数的性质,构造关于k的方程,解方程可求出k的值
(3)由(2)中结论,联立方程y=log2(2x+1)- x和y=
x和y= x+m,即2x•(2m-1)=1,分别讨论 m=0,m<0,m>0,三种情况下函数y=f(x)的图象与直线y=
x+m,即2x•(2m-1)=1,分别讨论 m=0,m<0,m>0,三种情况下函数y=f(x)的图象与直线y= x+m的图象交点个数,即可得到答案.
x+m的图象交点个数,即可得到答案.
解答:解:(1)∵z1=log2(2x+1)+ki,z2=1-xi
∴z1•z2=[log2(2x+1)+ki]•(1-xi)
=[log2(2x+1)+kx]+[k-x•log2(2x+1)+ki]i(2分)
f(x)=Re(z1•z2)=log2(2x+1)+kx(2分)
(2)设定义域R中任意实数,由函数f(x)是偶函数
得:f(-x)=f(x)(4分)
log2(2x+1)-kx=log2(2x+1)+kx
2kx=log2(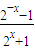 )=-x
)=-x
(2k+1)x=0
得:k=- (8分)
(8分)
证明:(3)由(2)得:f(x)=log2(2x+1)- x
x
联立方程:y=log2(2x+1)- x和y=
x和y= x+m
x+m
得:log2(2x+1)- x=
x= x+m (10分)
x+m (10分)
即m=log2(2x+1)-x
log2(2x+1)=x+m=log22(x+m)
得:2x+1=2(x+m)
2x•(2m-1)=1(11分)
若 m=0 方程无解(12分)
若 m<0,2m-1<0,2x<0方程无解(13分)
若m>0 2x=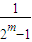
x=log2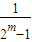
方程有唯一解(14分)
对任意实数m,函数y=f(x)的图象与直线y= x+m的图象的交点最多只有一个.(15分)
x+m的图象的交点最多只有一个.(15分)
点评:本题考查的知识点是函数的奇偶性的性质,函数解析式的求解方法,根的存在性及根的个数判断,是复数与函数三要素,性质,图象的综合应用,难度较大.
(2)根据函数f(x)是偶函数,根据偶函数的性质,构造关于k的方程,解方程可求出k的值
(3)由(2)中结论,联立方程y=log2(2x+1)-
 x和y=
x和y= x+m,即2x•(2m-1)=1,分别讨论 m=0,m<0,m>0,三种情况下函数y=f(x)的图象与直线y=
x+m,即2x•(2m-1)=1,分别讨论 m=0,m<0,m>0,三种情况下函数y=f(x)的图象与直线y= x+m的图象交点个数,即可得到答案.
x+m的图象交点个数,即可得到答案.解答:解:(1)∵z1=log2(2x+1)+ki,z2=1-xi
∴z1•z2=[log2(2x+1)+ki]•(1-xi)
=[log2(2x+1)+kx]+[k-x•log2(2x+1)+ki]i(2分)
f(x)=Re(z1•z2)=log2(2x+1)+kx(2分)
(2)设定义域R中任意实数,由函数f(x)是偶函数
得:f(-x)=f(x)(4分)
log2(2x+1)-kx=log2(2x+1)+kx
2kx=log2(
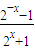 )=-x
)=-x(2k+1)x=0
得:k=-
 (8分)
(8分)证明:(3)由(2)得:f(x)=log2(2x+1)-
 x
x联立方程:y=log2(2x+1)-
 x和y=
x和y= x+m
x+m得:log2(2x+1)-
 x=
x= x+m (10分)
x+m (10分)即m=log2(2x+1)-x
log2(2x+1)=x+m=log22(x+m)
得:2x+1=2(x+m)
2x•(2m-1)=1(11分)
若 m=0 方程无解(12分)
若 m<0,2m-1<0,2x<0方程无解(13分)
若m>0 2x=
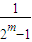
x=log2
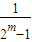
方程有唯一解(14分)
对任意实数m,函数y=f(x)的图象与直线y=
 x+m的图象的交点最多只有一个.(15分)
x+m的图象的交点最多只有一个.(15分)点评:本题考查的知识点是函数的奇偶性的性质,函数解析式的求解方法,根的存在性及根的个数判断,是复数与函数三要素,性质,图象的综合应用,难度较大.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目