题目内容
已知函数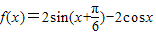 .
.(1)当
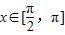 时,若
时,若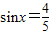 ,求函数f(x)的值;
,求函数f(x)的值;(2)当
 时,求函数
时,求函数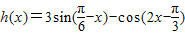 的值域;
的值域;(3)把函数y=f(x)的图象按向量
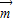 平移得到函数g(x)的图象,若函数g(x)是偶函数,写出
平移得到函数g(x)的图象,若函数g(x)是偶函数,写出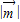 最小的向量
最小的向量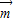 的坐标.
的坐标.
【答案】分析:(1)利用同角三角函数的基本关系 由sinx求出cosx,从而求得f(x)的值.
(2)根据x的范围,求得角x-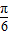 的范围,可得sin(x-
的范围,可得sin(x-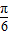 )的范围,利用两角差的正弦公式化简f(x)的解析式,
)的范围,利用两角差的正弦公式化简f(x)的解析式,
利用二次函数的性质求的h(x)的值域.
(3)根据向量平移得到g(x)的解析式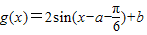 ,要使g(x)是偶函数,即要
,要使g(x)是偶函数,即要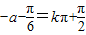 ,
,
求得a的解析式,通过|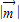 的解析式可得当k=-1时,
的解析式可得当k=-1时,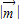 最小.
最小.
解答:解:(1)∵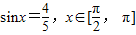 ,∴
,∴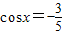 ,
,
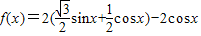 =
=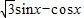 =
=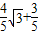 .
.
(2)∵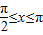 ,∴
,∴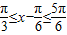 ,
, ,
,
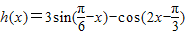 =
=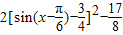
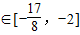 .
.
(3)设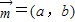 ,所以
,所以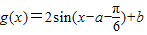 ,
,
要使g(x)是偶函数,即要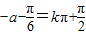 ,即
,即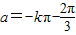 ,
,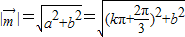 ,
,
当k=-1时,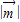 最小,此时
最小,此时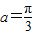 ,b=0,即向量
,b=0,即向量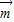 的坐标为
的坐标为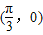 .
.
点评:本题考查同角三角函数的基本关系,两角差的正弦公式,正弦函数的定义域和值域,判断g(x)是偶函数 的条件,
是解题的难点.
(2)根据x的范围,求得角x-
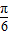 的范围,可得sin(x-
的范围,可得sin(x-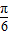 )的范围,利用两角差的正弦公式化简f(x)的解析式,
)的范围,利用两角差的正弦公式化简f(x)的解析式,利用二次函数的性质求的h(x)的值域.
(3)根据向量平移得到g(x)的解析式
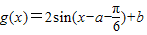 ,要使g(x)是偶函数,即要
,要使g(x)是偶函数,即要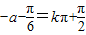 ,
,求得a的解析式,通过|
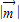 的解析式可得当k=-1时,
的解析式可得当k=-1时,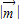 最小.
最小.解答:解:(1)∵
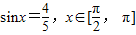 ,∴
,∴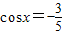 ,
,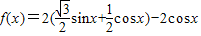 =
=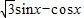 =
=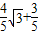 .
.(2)∵
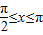 ,∴
,∴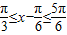 ,
, ,
,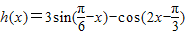 =
=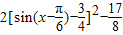
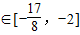 .
.(3)设
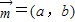 ,所以
,所以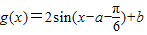 ,
,要使g(x)是偶函数,即要
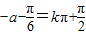 ,即
,即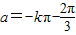 ,
,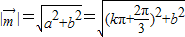 ,
,当k=-1时,
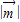 最小,此时
最小,此时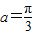 ,b=0,即向量
,b=0,即向量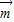 的坐标为
的坐标为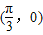 .
.点评:本题考查同角三角函数的基本关系,两角差的正弦公式,正弦函数的定义域和值域,判断g(x)是偶函数 的条件,
是解题的难点.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 .
.  时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式 的解集是
的解集是 ,求
,求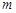 的取值范围.
的取值范围.
 。
。 时,判断
时,判断 的单调性;
的单调性; 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; .
. 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小;
的大小; (
( ).
).