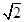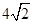题目内容
如图,动点P在正方体ABCD—A1B1C1D1的对角线BD1上,过点P作垂直于平面BB1D1D的直线,与正方体表面交于M、N,设BP=x,MN=y,则函数 的图象大致是
的图象大致是

B
解析只有当P移动到正方体中心O时,MN有唯一的最大值,则淘汰选项A、C;P点移动时,x与y的关系应该是线性的,则淘汰选项D.
解:设正方体的棱长为1,显然,当P移动到对角线BD1的中点O时,函数y=MN=AC= 取得唯一最大值,所以排除A、C;当P在BO上时,分别过M、N、P作底面的垂线,垂足分别为M1、N1、P1,
取得唯一最大值,所以排除A、C;当P在BO上时,分别过M、N、P作底面的垂线,垂足分别为M1、N1、P1,
则y=MN=M1N1=2BP1=2?xcos∠D1BD=2?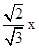 是一次函数,所以排除D.
是一次函数,所以排除D.
故选B.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为
A.1∶ | B.1∶9 | C. 1∶ 1∶ | D.1∶ |
若某几何体的三视图(单位:cm)如图所示,则几何体的体积为
A.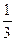 cm cm | B.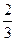 cm cm | C.1cm | D.2cm |
正三棱柱的底面边长为3,高为2,则其外接球的表面积为( )
| A. 4π | B. π π | C. π π | D.16π |
 )
) .
.





 ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
 的菱形,则该棱柱的体积等于 ( )
的菱形,则该棱柱的体积等于 ( )