题目内容
曲线C:f(x)=ex+sinx+1在x=0处的切线方程为________.
y=2x+2
分析:已知f(x)=ex+sinx+1对其进行求导,求在x=0处的斜率,根据点斜式,写出f(x)在点x=0处的切线方程.
解答:∵f(x)=ex+sinx+1,
∴f′(x)=ex+cosx,∴在x=0处的切线斜率k=f′(0)=1+1=2,
∴f(0)=1+0+1=2,
∴f(x)=ex+sinx+1在x=0处的切线方程为:y-2=2x,
∴y=2x+2,
故答案为:y=2x+2.
点评:此题主要考查利用导数研究曲线上莫点切线方程,解此题的关键是要对f(x)能够正确求导,此题是一道基础题.
分析:已知f(x)=ex+sinx+1对其进行求导,求在x=0处的斜率,根据点斜式,写出f(x)在点x=0处的切线方程.
解答:∵f(x)=ex+sinx+1,
∴f′(x)=ex+cosx,∴在x=0处的切线斜率k=f′(0)=1+1=2,
∴f(0)=1+0+1=2,
∴f(x)=ex+sinx+1在x=0处的切线方程为:y-2=2x,
∴y=2x+2,
故答案为:y=2x+2.
点评:此题主要考查利用导数研究曲线上莫点切线方程,解此题的关键是要对f(x)能够正确求导,此题是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
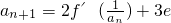 .求证:数列{an}中不存在成等差数列的三项;
.求证:数列{an}中不存在成等差数列的三项; .求证:数列{an}中不存在成等差数列的三项.
.求证:数列{an}中不存在成等差数列的三项.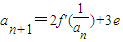 .求证:数列{an}中不存在成等差数列的三项.
.求证:数列{an}中不存在成等差数列的三项.