题目内容
选修4-1:几何证明选讲
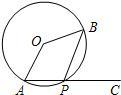
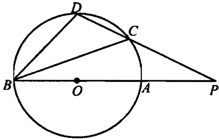
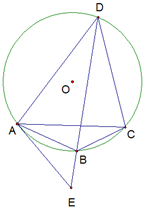
如图所示,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E.
(Ⅰ)求证:
=
;
(Ⅱ)求AD•AE的值.
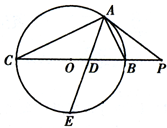
如图所示,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E.
(Ⅰ)求证:
| AB |
| AC |
| PA |
| PC |
(Ⅱ)求AD•AE的值.

( I)∵PA为⊙O的切线,
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA.…(2分)
∴
=
.…(3分)
( II)∵PA为⊙O的切线,PBC是过点O的割线,
∴PA2=PB•PC.…(5分)
又∵PA=10,PB=5,∴PC=20,BC=15.…(6分)
由( I)知,
=
=
,
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
,AB=3
…(7分)
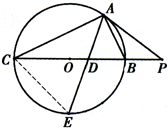
连接CE,则∠ABC=∠E,…(8分)
又∠CAE=∠EAB,
∴△ACE∽△ADB,
∴
=
…(9分)
∴AD•AE=AB•AC=3
×6
=90.…(10分)
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA.…(2分)
∴
| AB |
| AC |
| PA |
| PC |
( II)∵PA为⊙O的切线,PBC是过点O的割线,
∴PA2=PB•PC.…(5分)
又∵PA=10,PB=5,∴PC=20,BC=15.…(6分)
由( I)知,
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
| 5 |
| 5 |
连接CE,则∠ABC=∠E,…(8分)
又∠CAE=∠EAB,
∴△ACE∽△ADB,
∴
| AB |
| AE |
| AD |
| AC |
∴AD•AE=AB•AC=3
| 5 |
| 5 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,第二类在
,第二类在 ,第三类在
,第三类在 (单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.

 人,现用分层抽样的方法从该
人,现用分层抽样的方法从该



 的样本进行调查,其中从丙车间的产品中抽取了4件,则
的样本进行调查,其中从丙车间的产品中抽取了4件,则 .
.  则
则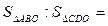 ____________.
____________.