题目内容
已知曲线C:(5-m)x2+(m-2)y2=8(m∈R)。
(1)若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2)设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G,求证:A,G,N三点共线。
(1)若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2)设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G,求证:A,G,N三点共线。
解:(1)原曲线方程可化简得: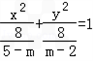
由题意,曲线C是焦点在x轴点上的椭圆可得: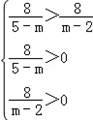 ,
,
解得: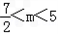 。
。
(2)证明:由已知直线代入椭圆方程化简得:(2k2+1)x2+16kx+24=0,
△=32(2k2-3)>0,
解得: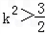
由韦达定理得: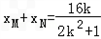 ①,
①,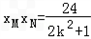 ,②
,②
设N(xN,kxN+4),M(xM,kxM+4),G(xG,1),
MB方程为: ,
,
则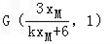 ,
,
∴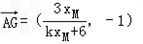 ,
,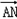 =(xN,kxN+2),
=(xN,kxN+2),
欲证A,G,N三点共线,只需证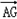 ,
,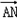 共线
共线
即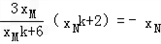 成立,
成立,
化简得:(3k+k)xMxN=-6(xM+xN)
将①②代入可得等式成立,则A,G,N三点共线得证。
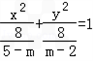
由题意,曲线C是焦点在x轴点上的椭圆可得:
 ,
,解得:
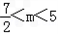 。
。(2)证明:由已知直线代入椭圆方程化简得:(2k2+1)x2+16kx+24=0,
△=32(2k2-3)>0,
解得:
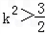
由韦达定理得:
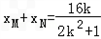 ①,
①,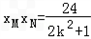 ,②
,②设N(xN,kxN+4),M(xM,kxM+4),G(xG,1),
MB方程为:
 ,
,则
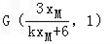 ,
,∴
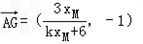 ,
,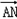 =(xN,kxN+2),
=(xN,kxN+2),欲证A,G,N三点共线,只需证
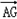 ,
,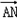 共线
共线即
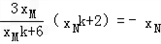 成立,
成立,化简得:(3k+k)xMxN=-6(xM+xN)
将①②代入可得等式成立,则A,G,N三点共线得证。

练习册系列答案
相关题目
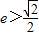 ,求m的取值范围;
,求m的取值范围;