Question

函数f（x）=|x|（|x-1|-|x+1|）是

1. A.
   是奇函数又是减函数
2. B.
   是奇函数但不是减函数
3. C.
   是减函数但不是奇函数
4. D.
   不是奇函数也不是减函数

Answer 1

A
分析：首先由奇函数的定义域关于原点对称，且满足f（-x）=-f（x），可判函数f（x）=|x|（|x-1|-|x+1|）是奇函数；
然后利用分类讨论的方法去绝对值符号，由于奇函数的图象关于原点对称，且对称两侧的单调性相同，所以只需讨论0≤x≤1与x＞1时即可；最后根据化简后的分段函数画出其图象，则f（x）的单调性一目了然．
解答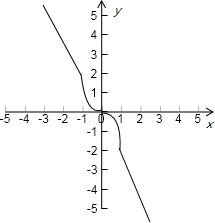：解：因为函数f（x）=的定义域关于原点对称，
且f（-x）=|-x|（|-x-1|-|-x+1|）=|x|（|x+1|-|x-1|）=-f（x），
所以f（x）是奇函数．
又因为当0≤x≤1时，f（x）=x（-x+1-x-1）=-2x²；
当x＞1时，f（x）=x（x-1-x-1）=-2x，
所以f（x）的图象如图：
所以f（x）既是奇函数，又是减函数．
故选A．
点评：本题考查函数的奇偶性定义及它的图象性质，同时考查数形结合的方法研究函数的单调性．