题目内容
设f(x)是定义域为(-∞,0)∪(0,+∞)的奇函数,且它在区间(-∞,0)上单调增。
(1)用定义证明:f(x)在(0,+∞)上的单调性;
(2)若mn<0且m+n<0,试判断f(m)+f(n)的符号;
(3)若f(1)=0,解关于x的不等式f[loga(x-1)+1]>0。
(1)用定义证明:f(x)在(0,+∞)上的单调性;
(2)若mn<0且m+n<0,试判断f(m)+f(n)的符号;
(3)若f(1)=0,解关于x的不等式f[loga(x-1)+1]>0。
(1)证明:设 ,且
,且 ,
,
则 ,且
,且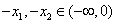 ,
,
由已知函数在(-∞,0)上单调递增,得: ,
,
又函数是奇函数,有 ,即
,即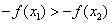 ,
,
得到: ,所以函数在(0,+∞)上递增函数。
,所以函数在(0,+∞)上递增函数。
(2)解:不妨设m>0,n<0,
则由已知m+n<0 0<m<-n,
0<m<-n,
已知函数在(0,+∞) 上递增,
故有:f(m)<f(-n)=-f(n),得f(m)+f(n)<0。
(3)由 及函数在(-∞,0)和(0,+∞)上递增,
及函数在(-∞,0)和(0,+∞)上递增,
可知: 或
或 ,
,
即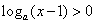 或
或 ,
,
当a>1时,x>2或 ;
;
当0<a<1时,1<x<2或 ;
;
综上所述:当a>1时,不等式的解集为{x| x>2或 };
};
当0<a<1时,不等式的解集为{x|1<x<2或 }。
}。
 ,且
,且 ,
,则
 ,且
,且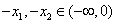 ,
,由已知函数在(-∞,0)上单调递增,得:
 ,
,又函数是奇函数,有
 ,即
,即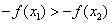 ,
,得到:
 ,所以函数在(0,+∞)上递增函数。
,所以函数在(0,+∞)上递增函数。 (2)解:不妨设m>0,n<0,
则由已知m+n<0
 0<m<-n,
0<m<-n,已知函数在(0,+∞) 上递增,
故有:f(m)<f(-n)=-f(n),得f(m)+f(n)<0。
(3)由
 及函数在(-∞,0)和(0,+∞)上递增,
及函数在(-∞,0)和(0,+∞)上递增,可知:
 或
或 ,
,即
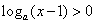 或
或 ,
,当a>1时,x>2或
 ;
;当0<a<1时,1<x<2或
 ;
;综上所述:当a>1时,不等式的解集为{x| x>2或
 };
};当0<a<1时,不等式的解集为{x|1<x<2或
 }。
}。 
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,则f(-
,则f(- 则f(
则f( 的函数,若f(x)=
的函数,若f(x)= ,则f
,则f
