题目内容
已知数列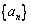 中,
中, ,
,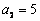 ,其前
,其前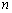 项和
项和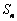 满足
满足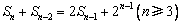 .令
.令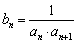 .
.
(Ⅰ)求数列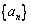 的通项公式;
的通项公式;
(Ⅱ)若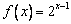 ,求证:
,求证: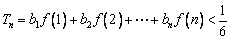 (
(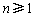 );
);
(Ⅲ)令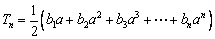 (
(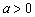 ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有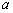 的值:①对于任意正整数
的值:①对于任意正整数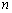 ,都有
,都有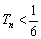 ;②对于任意的
;②对于任意的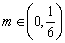 ,均存在
,均存在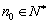 ,使得
,使得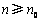 时,
时,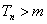 .
.
【答案】
解(Ⅰ)由题意知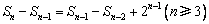 即
即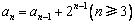 ……1′
……1′
∴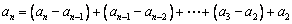
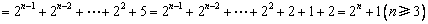 ……3′
……3′
检验知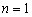 、
、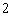 时,结论也成立,故
时,结论也成立,故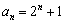 .…………4′
.…………4′
法二: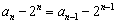
法三: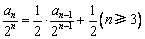
(Ⅱ)由于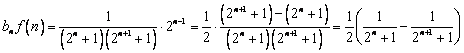
故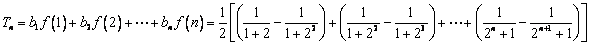
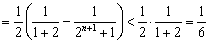 .…………9′
.…………9′
(Ⅲ)(ⅰ)当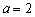 时,由(Ⅱ)知:
时,由(Ⅱ)知: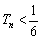 ,即条件①满足;又
,即条件①满足;又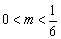 ,
,
∴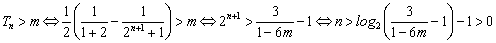 .
.
取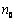 等于不超过
等于不超过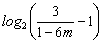 的最大整数,则当
的最大整数,则当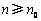 时,
时,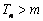 .…10′
.…10′
(ⅱ)当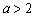 时,∵
时,∵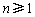 ,
,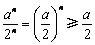 ,∴
,∴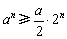 ,∴
,∴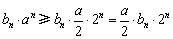 .
.
∴ .
.
由(ⅰ)知存在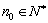 ,当
,当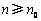 时,
时,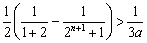 ,
,
故存在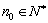 ,当
,当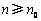 时,
时,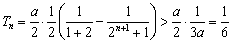 ,不满足条件. …12′
,不满足条件. …12′
(ⅲ)当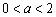 时,∵
时,∵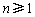 ,
,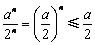 ,∴
,∴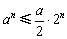 ,∴
,∴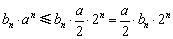 .
.
∴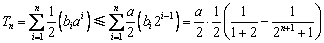 .
.
取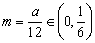 ,若存在
,若存在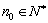 ,当
,当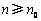 时,
时,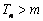 ,则
,则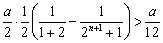 .
.
∴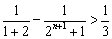 矛盾. 故不存在
矛盾. 故不存在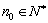 ,当
,当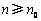 时,
时,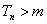 .不满足条件.
.不满足条件.
综上所述:只有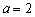 时满足条件,故
时满足条件,故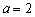 .…………14′
.…………14′

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
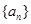 中,
中,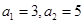 ,
,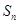 为其前n项和,且满足
为其前n项和,且满足
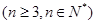 。
。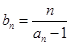 ,求数列
,求数列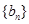 的前n项和
的前n项和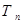 ;
;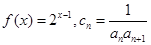 ,
,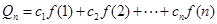 ,求证
,求证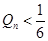 (n∈N*)。
(n∈N*)。