题目内容
已知函数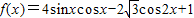 ,且给定条件p:“
,且给定条件p:“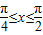 ”.
”.(1)求f(x)在给定条件p下的最大值及最小值;
(2)若又给条件q:“|f(x)-m|<2“,且p是q的充分不必要条件,求实数m的取值范围.
【答案】分析:(1)先根据二倍角公式和辅助角公式进行化简,再由x的范围求出2x- 的范围,再结合正弦函数的性质可求出其最大、最小值.
的范围,再结合正弦函数的性质可求出其最大、最小值.
(2)先根据|f(x)-m|<2求出f(x)的范围,再由p是q的充分条件和(1)中f(x)的最大、最小值可得到m的范围.
解答:解:(1)∵f(x)=2sin2x-2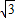 cos2x+1
cos2x+1
=4sin(2x-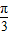 )+1.
)+1.
又∵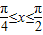 ,
,
∴ ≤2x-
≤2x-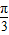 ≤
≤ ,
,
即3≤4sin(2x-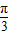 )+1≤5
)+1≤5
∴f(x)max=5,f(x)min=3
(2)∵|f(x)-m|<2,
∴m-2<f(x)<m+2
又p是q的充分不必要条件
∴ ,
,
∴3<m<5.
∴m的取值范围为(3,5)
点评:本题主要考查两角和与差的公式的逆用和正弦函数的性质,同时考查了运算求解的能力,属于中档题.
 的范围,再结合正弦函数的性质可求出其最大、最小值.
的范围,再结合正弦函数的性质可求出其最大、最小值.(2)先根据|f(x)-m|<2求出f(x)的范围,再由p是q的充分条件和(1)中f(x)的最大、最小值可得到m的范围.
解答:解:(1)∵f(x)=2sin2x-2
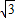 cos2x+1
cos2x+1=4sin(2x-
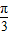 )+1.
)+1.又∵
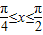 ,
,∴
 ≤2x-
≤2x-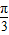 ≤
≤ ,
,即3≤4sin(2x-
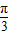 )+1≤5
)+1≤5∴f(x)max=5,f(x)min=3
(2)∵|f(x)-m|<2,
∴m-2<f(x)<m+2
又p是q的充分不必要条件
∴
 ,
,∴3<m<5.
∴m的取值范围为(3,5)
点评:本题主要考查两角和与差的公式的逆用和正弦函数的性质,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
 ,且给定条件p:
,且给定条件p: .
. ,且给定条件p:
,且给定条件p: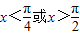 .
. ,且给定条件p:“
,且给定条件p:“ ”,
”,