题目内容
已知函数f(x)=2ax- -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0)
(Ⅰ)当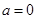 时,求
时,求 的极值;
的极值;
(Ⅱ)当a>0时,讨论 的单调性;
的单调性;
(Ⅲ)若对任意的a∈(2,3),x1,x2∈[1,3],恒有 成立,求实数m的取值范围。
成立,求实数m的取值范围。
(Ⅰ) 的极大值为
的极大值为 ,无极小值;(Ⅱ)①当
,无极小值;(Ⅱ)①当 时,
时, 在
在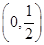 和
和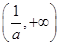 上是增函数,在
上是增函数,在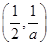 上是减函数;②当
上是减函数;②当 时,
时, 在
在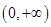 上是增函数;③当
上是增函数;③当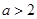 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 ; (Ⅲ)
上是减函数 ; (Ⅲ)
【解析】
试题分析:(Ⅰ)当 时,求
时,求 的极值,首先确定函数的定义域为
的极值,首先确定函数的定义域为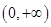 ,对函数
,对函数 求导函数
求导函数 ,确定函数的单调性,即可求得函数
,确定函数的单调性,即可求得函数 的极值;(Ⅱ)当a>0时,讨论
的极值;(Ⅱ)当a>0时,讨论 的单调性,首先对函数
的单调性,首先对函数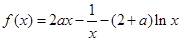 求导函数
求导函数 ,并分解得
,并分解得 ,再进行分类讨论,利用
,再进行分类讨论,利用 ,确定函数单调减区间;
,确定函数单调减区间; ,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有
,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有 成立,只要求出
成立,只要求出 的最大值即可,因此确定函数
的最大值即可,因此确定函数 在
在 上单调递减,可得
上单调递减,可得 的最大值与最小值,从而得
的最大值与最小值,从而得 ,进而利用分离参数法,可得
,进而利用分离参数法,可得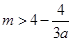 ,从而可求实数
,从而可求实数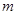 的取值范围
的取值范围
试题解析:(Ⅰ)当 时,
时,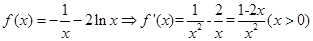 2分
2分
由 ,解得
,解得 ,可知
,可知 在
在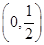 上是增函数,在
上是增函数,在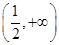 上是减函数 4分
上是减函数 4分
∴ 的极大值为
的极大值为 ,无极小值
5分
,无极小值
5分
(Ⅱ) ,
,
①当 时,
时, 在
在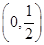 和
和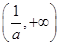 上是增函数,在
上是增函数,在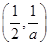 上是减函数; 7分
上是减函数; 7分
②当 时,
时, 在
在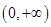 上是增函数;
8分
上是增函数;
8分
③当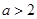 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 9分
上是减函数 9分
(Ⅲ)当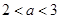 时,由(2)可知
时,由(2)可知 在
在 上是增函数,
上是增函数,
∴ 10分
10分
由 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
∴ 11分
11分
即 对任意
对任意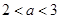 恒成立,
恒成立,
即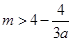 对任意
对任意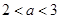 恒成立,
12分
恒成立,
12分
由于当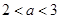 时,
时, ,∴
,∴ 14分
14分
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性;函数在某点取得极值的条件

