题目内容
已知a和b是任意非零实数.(1)求
| |2a+b|+|2a-b| | |a| |
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,求实数x的取值范围.
分析:(1)利用绝对值不等式的性质可得
≥
=
=4.
(2)由题意可得|2+x|+|2-x|≤
恒成立,由于
的最小值为4,故有x的
范围即为不等式|2+x|+|2-x|≤4的解集,解绝对值不等式求得实数x的取值范围.
| |2a+b|+|2a-b| |
| |a| |
| |2a+b+2a-b| |
| |a| |
| |4a| |
| |a| |
(2)由题意可得|2+x|+|2-x|≤
| |2a+b|+|2a-b| |
| |a| |
| |2a+b|+|2a-b| |
| |a| |
范围即为不等式|2+x|+|2-x|≤4的解集,解绝对值不等式求得实数x的取值范围.
解答:解:(1)∵
≥
=
=4,
故
的最小值为4.
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,
即|2+x|+|2-x|≤
恒成立,故|2+x|+|2-x|不大于
的最小值.(4分)
由(1)可知,
的最小值为4,当且仅当(2a+b)(2a-b)≥0时取等号,
∴
的最小值等于4.(8分)
∴x的范围即为不等式|2+x|+|2-x|≤4的解集.
解不等式得-2≤x≤2,故实数x的取值范围为[-2,2]. (10分)
| |2a+b|+|2a-b| |
| |a| |
| |2a+b+2a-b| |
| |a| |
| |4a| |
| |a| |
故
| |2a+b|+|2a-b| |
| |a| |
(2)若不等式|2a+b|+|2a-b|≥|a|(|2+x|+|2-x|)恒成立,
即|2+x|+|2-x|≤
| |2a+b|+|2a-b| |
| |a| |
| |2a+b|+|2a-b| |
| |a| |
由(1)可知,
| |2a+b|+|2a-b| |
| |a| |
∴
| |2a+b|+|2a-b| |
| |a| |
∴x的范围即为不等式|2+x|+|2-x|≤4的解集.
解不等式得-2≤x≤2,故实数x的取值范围为[-2,2]. (10分)
点评:本题考查查绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
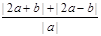 的最小值.
的最小值.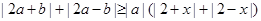 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.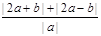 的最小值。
的最小值。 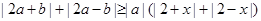 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.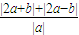 的最小值.
的最小值.