题目内容
某家具厂有方木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m2,五合板1m2,出售一张方桌可获利润80元,出售一个书橱可获利润120元.怎样安排生产可使所得利润最大?最大利润为多少?
解:
设生产书桌x张,书橱y个,利润总额为z元.………………1分
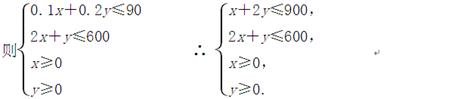
z=80x+120y. ………………………………3分
在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域.
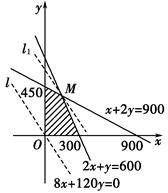 ……………………………………………5分
……………………………………………5分
作直线l:80x+120y=0,即直线l:2x+3y=0.
把直线l向右上方平移至l1的位置时,直线经过可行域上的点M,
此时z=80x+120y取得最大值.…………………7分

∴当x=100,y=400时,zmax=80×100+120×400=56000(元).………10分
因此,生产书桌100张、书橱400个,可使所得利润最大最大利润为56000元
设生产书桌x张,书橱y个,利润总额为z元.………………1分
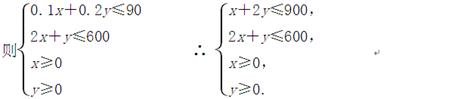
z=80x+120y. ………………………………3分
在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域.
 ……………………………………………5分
……………………………………………5分作直线l:80x+120y=0,即直线l:2x+3y=0.
把直线l向右上方平移至l1的位置时,直线经过可行域上的点M,
此时z=80x+120y取得最大值.…………………7分

∴当x=100,y=400时,zmax=80×100+120×400=56000(元).………10分
因此,生产书桌100张、书橱400个,可使所得利润最大最大利润为56000元
本试题主要考查了线性规划的最优解问题,研究实际问题中的利润最大的运用试题,首先是作出可行域满足的不等式组,然后作图,平移得到结论。

练习册系列答案
相关题目
 为直角坐标系原点,
为直角坐标系原点,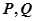 坐标均满足不等式组
坐标均满足不等式组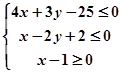 ,则使
,则使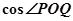 取最小值时的
取最小值时的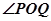 的大小为_____________.
的大小为_____________. 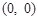 和点
和点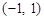 在直线
在直线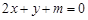 的同侧,则
的同侧,则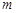 的取值范围 ( ).
的取值范围 ( ).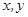 满足
满足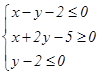 ,则
,则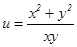 的取值范围是( )
的取值范围是( )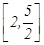
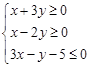 ,则x2+y2的最大值是____.
,则x2+y2的最大值是____.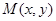 的坐标满足不等式组
的坐标满足不等式组 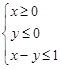 ,点
,点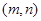 在点
在点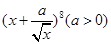 展开式中,中间项的系数为70.若实数
展开式中,中间项的系数为70.若实数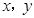 满足
满足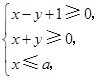 则
则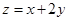 的最小值是( )
的最小值是( )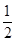
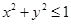 ,则点
,则点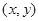 不在区域
不在区域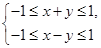 内的概率是( )
内的概率是( )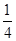
 满足约束条件:
满足约束条件: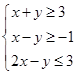 ,则目标函数
,则目标函数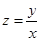 的最小值为 .
的最小值为 .