题目内容
已知双曲线的两条渐近线方程为直线l1:y=-| x |
| 2 |
| x |
| 2 |
| 3 |
(1)求双曲线方程;
(2)设P1,P2分别是直线l1和l2上的点,点M在双曲线上,且
| P1M |
| MP2 |
分析:(1)先依题意可设双曲线方程,利用实轴长为2
,求得参数,从而写出双曲线方程;
(2)设P1(-2y1,y1),P2(2y2,y2)和点M(x0,y0)利用向量条件以及M在双曲线上得到三点的坐标之间的关系式,整理得y1y2=
,又直线P1P2的方程为
=
令x=0得y=
最后利用三角形面积公式求三角形P1OP2的面积即得.
| 3 |
(2)设P1(-2y1,y1),P2(2y2,y2)和点M(x0,y0)利用向量条件以及M在双曲线上得到三点的坐标之间的关系式,整理得y1y2=
| 27 |
| 8 |
| y-y1 |
| y2-y1 |
| x+2y1 |
| 2y2+2y1 |
| 2y1y2 |
| y1+y2 |
解答:解:(1)依题意可设双曲线方程为:y2-
=λ(λ>0)即
-
=1
则2
=2
∴λ=3∴双曲线方程为
-
=1…(5分)
(2)设P1(-2y1,y1),P2(2y2,y2)和点M(x0,y0)∵
=2
∴
又∵M在双曲线上∴
-
=3∴(
)2-
(
)2=3整理得y1y2=
…(9分)
又直线P1P2的方程为
=
令x=0得y=
∴S△P1OP2=
•|
|•|(2y2+2y1)|=2|y1y2|=
…(13分)
| x2 |
| 4 |
| y2 |
| λ |
| x2 |
| 4λ |
则2
| λ |
| 3 |
| y2 |
| 3 |
| x2 |
| 12 |
(2)设P1(-2y1,y1),P2(2y2,y2)和点M(x0,y0)∵
| P1M |
| MP2 |
|
| y | 2 0 |
| ||
| 4 |
| y1+2y2 |
| 3 |
| 1 |
| 4 |
| -2y1+4y2 |
| 3 |
| 27 |
| 8 |
又直线P1P2的方程为
| y-y1 |
| y2-y1 |
| x+2y1 |
| 2y2+2y1 |
| 2y1y2 |
| y1+y2 |
| 1 |
| 2 |
| 2y1y2 |
| y1+y2 |
| 27 |
| 4 |
点评:本小题主要考查双曲线的标准方程、双曲线的简单性质、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,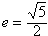 。
。