题目内容
与函数y=e2x-2ex+1(x≥0)的曲线关于直线y=x对称的曲线的方程为( )
A、y=ln(1+
| ||
B、y=ln(1-
| ||
C、y=-ln(1+
| ||
D、y=-ln(1-
|
分析:求函数y=e2x-2e2+1反函数即可.
解答:解:由题意
∵y=e2x-2ex+1(x≥0)?(ex-1)2=y
∵x≥0,∴ex≥1,即ex=1+
∴x=ln(1+
),
所以f-1(x)=ln(1+
)
故选A.
∵y=e2x-2ex+1(x≥0)?(ex-1)2=y
∵x≥0,∴ex≥1,即ex=1+
| y |
| y |
所以f-1(x)=ln(1+
| x |
故选A.
点评:本题考查了方程和函数的关系以及反函数的求解.同时还考查了转化能力.

练习册系列答案
相关题目
若函数y=f(x)的图象与函数y=ln
+1的图象关于直线y=x对称,则f(x)=( )
| x |
| A、e2x-2 |
| B、e2x |
| C、e2x+1 |
| D、e2x+2 |
若函数y=f(x+1)与y=e2x+2的图象关于直线y=x对称,则f(x)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
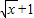 的图象关于直线y=x对称,则f(x)=( )
的图象关于直线y=x对称,则f(x)=( )