题目内容
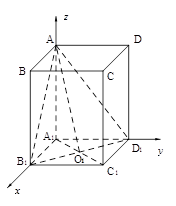
(理科)已知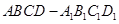 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,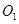 是
是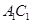 和
和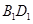 的交点.
的交点.
⑴设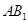 与底面
与底面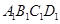 所成的角的大小为
所成的角的大小为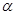 ,二面角
,二面角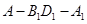 的大小为
的大小为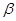 ,试确定
,试确定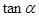 与
与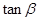 的一个等量关系,并给出证明;
的一个等量关系,并给出证明;
⑵若点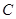 到平面
到平面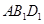 的距离为
的距离为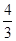 ,求正四棱柱
,求正四棱柱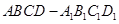 的高.
的高.
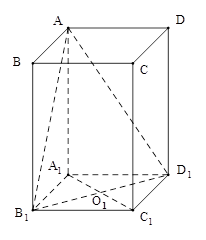
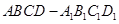 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,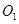 是
是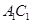 和
和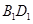 的交点.
的交点.⑴设
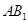 与底面
与底面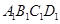 所成的角的大小为
所成的角的大小为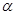 ,二面角
,二面角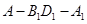 的大小为
的大小为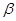 ,试确定
,试确定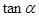 与
与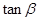 的一个等量关系,并给出证明;
的一个等量关系,并给出证明;⑵若点
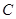 到平面
到平面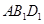 的距离为
的距离为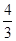 ,求正四棱柱
,求正四棱柱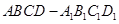 的高.
的高.
解:设正四棱柱的高为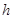 .
.
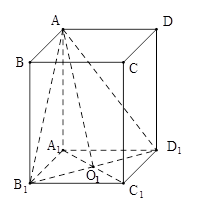
⑴ 连 ,
,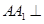 底面
底面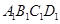 于
于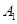 ,∴
,∴ 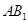 与底面
与底面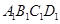 所成的角为
所成的角为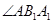 ,即
,即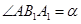 .
.
∵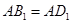 ,
,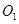 为
为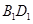 中点,∴
中点,∴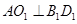 ,又
,又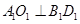 ,
,
∴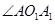 是二面角
是二面角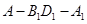 的平面角,即
的平面角,即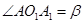 .
.
∴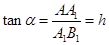 ,
,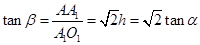 .
.
⑵ 建立如图空间直角坐标系,有
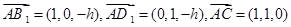
设平面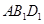 的一个法向量为
的一个法向量为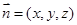 ,
,
∵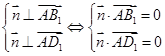 ,取
,取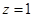 得
得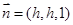
∴ 点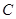 到平面
到平面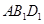 的距离为
的距离为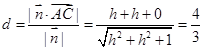 ,则
,则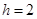 .
.
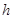 .
.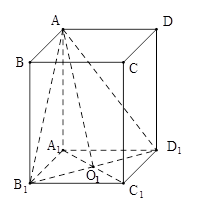
⑴ 连
 ,
,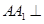 底面
底面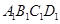 于
于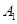 ,∴
,∴ 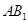 与底面
与底面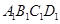 所成的角为
所成的角为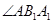 ,即
,即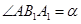 .
.∵
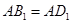 ,
,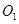 为
为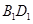 中点,∴
中点,∴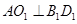 ,又
,又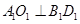 ,
,∴
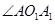 是二面角
是二面角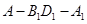 的平面角,即
的平面角,即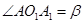 .
.
∴
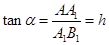 ,
,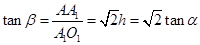 .
.⑵ 建立如图空间直角坐标系,有

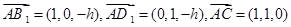
设平面
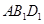 的一个法向量为
的一个法向量为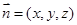 ,
,∵
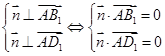 ,取
,取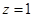 得
得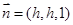
∴ 点
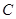 到平面
到平面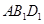 的距离为
的距离为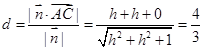 ,则
,则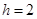 .
.略

练习册系列答案
相关题目




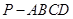 的底面为直角梯形,
的底面为直角梯形,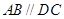 ,
,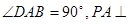 底面
底面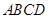 ,且
,且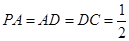 ,
,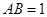 ,
,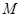 是
是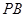 的中点。
的中点。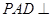 面
面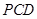 ;
;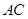 与
与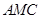 与面
与面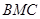 所成二面角的余弦值。
所成二面角的余弦值。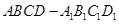 的棱长为
的棱长为 ,则点
,则点 到
到 的距离为_____________.
的距离为_____________. 
 (
( )定义其“调和均数倒数”
)定义其“调和均数倒数” (
( 时,
时,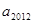 =_______________.
=_______________. ,
,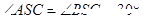 ,则棱锥S-ABC的体积为 ( )
,则棱锥S-ABC的体积为 ( )

