题目内容
(本小题满分13分)
已知常数a为正实数,曲线Cn:y=在其上一点Pn(xn,yn)的切线ln总经过定点(-a,0)(n∈N*).
(1)求证:点列:P1,P2,…,Pn在同一直线上;
(2)求证: (n∈N*).
(n∈N*).
证法一:(1)∵f(x)=,
∴f′(x)=·(nx)′=·.(1分)
Cn:y=在点Pn(xn,yn)处的切线ln的斜率kn=f′(xn)=·,
∴ln的方程为y-yn=·(x-xn).(2分)
∵ln经过点(-a,0),
∴yn=-·(-a-xn)=·(a+xn).
又∵Pn在曲线Cn上,∴yn==·(a+xn),
∴xn=a,∴yn=,∴Pn(a,)总在直线x=a上,
即P1,P2,…,Pn在同一直线x=a上.(4分)
(2)由(1)可知yn=,∴f(i)===.(5分)
=<=2(-)(i=1,2,…,n),
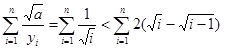
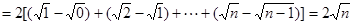 .(9分)
.(9分)
设函数F(x)=-ln(x+1),x∈[0,1],有F(0)=0,
∴F′(x)=-==>0(x∈(0,1)),
∴F(x)在[0,1]上为增函数,
即当0<x<1时F(x)>F(0)=0,故当0<x<1时>ln(x+1)恒成立.(11分)
取x=(i=1,2,3,…,n),f(i)=>ln(1+)=ln(i+1)-lni,
即f(1)=>ln2,f(2)=>ln(1+)=ln3-ln2,…,f(n)=>ln(n+1)-lnn,
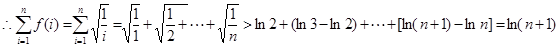 综上所述有
综上所述有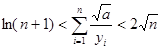 (n∈N*).(13分)
(n∈N*).(13分)
证法二:(1)设切线ln的斜率为kn,由切线过点(-a,0)得切线方程为y=kn(x+a),
则方程组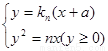 的解为
的解为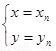 .(1分)
.(1分)
由方程组用代入法消去y化简得kx2+(2ak-n)x+ka2=0,(*)
有Δ=(2ak-n)2-4k·ka2=-4ank+n2=0,
∴k=.(2分)
代入方程(*),得x2+(2a·-n)x+·a2=0,即x2-2a·x+a2=0,
∴x=a,即有xn=a,yn==,
即P1,P2,…,Pn在同一直线x=a上.(4分)
(2)先证:0<x<1时>x>ln(x+1),以下类似给分
【解析】略


 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和