题目内容
已知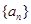
是递增的等比数列，若
，
，则此数列的公比
．
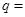2
解析试题分析：由已知{an}是递增等比数列，，我们可以判断此数列的公比q＞1，又由，，我们可以构造出一个关于公比q的方程，解方程即可求出公比q的值．：∵{an}是递增等比数列，且，则公比q＞1，又∵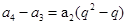
=2（q2-q）=4，即q2-q-2=0，解得q=2，或q=-1（舍去），，故此数列的公比q=2，故答案为：2
考点：等比数列的性质
点评：本题考查的知识点是等比数列的通项公式，其中利用等比数列的通项公式及，，构造出一个关于公比q的方程，是解答本题的关键．
练习册系列答案
相关题目
与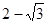
的等比中项为________________。
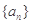中，若
，
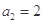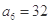，则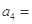
}是公比为正数 的等比数列，若
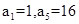，则数列{
中，
，公比
，若
，则
的值为 ．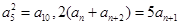
，则数列｛an｝的通项公式an =______________。
的公比
大于1，若向量
，
，满足
,则
_____________
的前n项和为
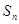
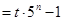，则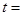
所有项均为正数，首
，且
成等差数列．
的前n项和为
，若
，求实数
的值．