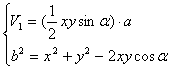Question

小强家住在农村，十月一日，国庆节放假回家，正赶上父亲收割庄稼，由于今年大丰收粮食太多，自家的谷仓已全部装满，还剩下很多.这时爸爸想出了一个主意，决定用一个长方形木板，借助两面墙，在西屋的墙角处围了一个直三棱柱的谷仓，木板可立，可.小强心想，这么多的粮食，怎样围才能装最多的粮食呢？经过测量和运算，小强得到了满意的方案，向父亲提供了建议.请你叙述小强的作法.如果换成任意的两面墙，如何处理？

 

Answer 1

答案：
解析：

显然，围成直三棱柱的底面为直角三角形，若两直角边分别为x和y,则x2+y2是长方形木板的长或宽(定值）的平方.这样，本例的问题主要体现在均值不等式的应用上. 解：一）.小强用直尺测出木板的长为a,宽为b，依题可知：a>b>0，且两墙夹角(即二面角）为90°. (1)a作底边,设S底为底面直角三角形的面积,两直角边一个是x,一个是y,则有: S底=xy,V1=(xy)·b,且x2+y2=a2 ∵x2+y2≥2xy ∴xy≤ ∴V1≤,当且仅当x=y=a时取“=”号. (2)b作底边，同(1)可得V2≤,当且仅当x=y=b时取“=”号. 又a>b>0  ∴ab>0,a－b>0 ∴V1－V2=－=ab(a－b)>0 ∴V1>V2,即> 故把长方形木板的长边放在底面，且围成的直三棱柱的底面是等腰直角三角形时，容积最大. 二）.若两面夹角(即二面角)换成α时，解答如下： (1)设用矩形木板长a作直三棱柱的侧棱，宽b作为底面的一条边，底面三角形的另两边的长分别是x,y,体积为V1，则有： ∴xy=,x2+y2=b2+≥2xy ∴b2+≥   整理得： V1≤ab2·cot,当x=y时取“=”号.   (2)设矩形木板的宽b作侧棱，则 当x=y时，V2=a2b·cot. ∵a>b>0,∴ab>0,a－b>0 ∴a2b>ab2  即V2>V1 < 故把矩形木板的长边放在底面，且围成的直三棱柱的底面是等腰三角形(顶角为α)时，容积最大，且最大值Vmax=a2b·cot.