Question

将直线l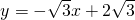：绕点（2，0）按顺时针方向旋转60°得到直线l′，则直线l′的方程是________．

Answer 1

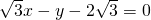
分析：由题意可得直线l′的倾斜角等于120°-60°=60°，故直线l′的斜率为tan60°=，再由点斜式求得直线l′的方程．
解答：由于直线l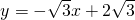：的斜率为-，倾斜角等于120°，
把它绕点（2，0）按顺时针方向旋转60°得到直线l′，
则直线l′的倾斜角等于120°-60°=60°，故直线l′的斜率为tan60°=．
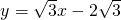由点斜式求得直线l′的方程是y-0=（x-2），即 ，即 ，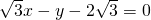
故答案为 ．
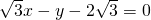点评：本题主要考查直线的倾斜角和斜率的关系，用点斜式求直线方程，求得直线l′的斜率为tan60°=，是解题的关键，属于中档题．