题目内容
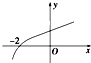
已知函数y=lg(x+a)的图象如图所示,则a的值为( )

| A、2 | B、3 | C、4 | D、5 |
分析:根据对数函数图象必过定点(1,0),利用函数图象的平移变换得到函数y=lg(x+a)的图象必过定点(1-a,0),结合题中图象,即可得到a的值、
解答:解:∵函数y=lg(x+a)的图象是由函数y=lgx向左平移了a个单位得到的,
而y=lgx的图象必过定点(1,0),
∴函数y=lg(x+a)的图象必过定点(1-a,0),
又根据题中所给的函数y=lg(x+a)的图象,
∴函数y=lg(x+a)的图象过定点(-2,0),
∴1-a=-2,
解得a=3,
∴a的值为3.
故选:B.
而y=lgx的图象必过定点(1,0),
∴函数y=lg(x+a)的图象必过定点(1-a,0),
又根据题中所给的函数y=lg(x+a)的图象,
∴函数y=lg(x+a)的图象过定点(-2,0),
∴1-a=-2,
解得a=3,
∴a的值为3.
故选:B.
点评:本题考查了对数函数的图象与性质.对数函数的图象恒过定点(1,0),且它的单调性与底数a的取值有关,当a>1时,函数单调递增,当0<a<1时,函数单调递减.本题解题的关键是函数恒过的定点也跟着图象的平移而平移.属于基础题.

练习册系列答案
相关题目