题目内容
已知平面α的一个法向量是 =(1,1,-1),且平面α经过点A(1,2,0).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是________.
=(1,1,-1),且平面α经过点A(1,2,0).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是________.
x+y-z-3=0
分析:求出向量 ,利用平面α的一个法向量是
,利用平面α的一个法向量是 =(1,1,-1),通过向量的数量积为0,求解即可.
=(1,1,-1),通过向量的数量积为0,求解即可.
解答:由题意可知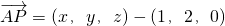 =(x-1,y-2,z);
=(x-1,y-2,z);
平面α的一个法向量是 =(1,1,-1),所以
=(1,1,-1),所以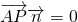 ,
,
即:(x-1,y-2,z)(1,1,-1)=0;
x-1+y-2-z=0,即x+y-z-3=0,
所求点P的坐标满足的方程是x+y-z-3=0.
故答案为:x+y-z-3=0.
点评:本题是基础题,考查点的轨迹方程的求法,注意向量的数量积的应用,考查计算能力.
分析:求出向量
 ,利用平面α的一个法向量是
,利用平面α的一个法向量是 =(1,1,-1),通过向量的数量积为0,求解即可.
=(1,1,-1),通过向量的数量积为0,求解即可.解答:由题意可知
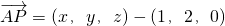 =(x-1,y-2,z);
=(x-1,y-2,z);平面α的一个法向量是
 =(1,1,-1),所以
=(1,1,-1),所以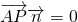 ,
,即:(x-1,y-2,z)(1,1,-1)=0;
x-1+y-2-z=0,即x+y-z-3=0,
所求点P的坐标满足的方程是x+y-z-3=0.
故答案为:x+y-z-3=0.
点评:本题是基础题,考查点的轨迹方程的求法,注意向量的数量积的应用,考查计算能力.

练习册系列答案
相关题目
 =(1,1,-1),且平面α经过点A(1,2,0).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是 .
=(1,1,-1),且平面α经过点A(1,2,0).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是 .