题目内容
利用函数的单调性定义研究函数f(x)=
在定义域内的单调性.
思路解析:首先确定定义域;再在R上任取x1,x2,且x1＜x2;再作差f(x1)-f(x2);再对差式进行分子有理化的变形,其关键是分子有理化的变形. 解:∵定义域是x≥-1,∴任意选取x1、x2,使-1≤x1＜x2,则f(x1)= ∴f(x1)-f(x2)= ∵-1≤x1＜x2,∴x1-x2＜0.∴ ∴函数f(x)= 深化升华 (1)在利用函数单调性的定量化定义证明函数的单调性时,变形和定号是关键的两步.变形的目的不是化简而是为了定号,应该变形到非常容易说明差的符号的形式为止,变形不充分不到位,则不易定号. (2)为了达到定号的目的,注意一些变形的常用的技巧,像通分、分解因式、分子有理化等. 方法归纳 利用函数定量化的严格定义,证明函数的单调性是我们研究函数单调性的一种重要方法,在证明的过程中,选取自变量的两个一大一小值后,比较这两个自变量的值所对应的函数值的大小是证明的关键,其中“作差”比较大小是我们的一个常用方法.利用单调性的定量定义证明函数单调性的步骤是: ①任取→②作差→③变形→④定号. 利于定义研究有理函数单调性时,经常的变形方法是通分,分解因式；对无理函数经常的变形方法是分子或分母有理化.,f(x2)=
.
-
=
.
＜0,即f(x1)＜f(x2).
在定义域内是增函数.
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
)上是减函数.
.利用函数的单调性定义证明函数F(x)是R上的减函数. 
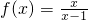，x∈[2，4]是单调递减函数，并求函数的值域．