题目内容
已知函数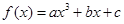 在
在 处取得极值
处取得极值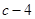 .
.
(1)求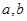 ;
;
(2)设函数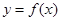 为R上的奇函数,求函数
为R上的奇函数,求函数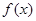 在区间
在区间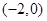 上的极值.
上的极值.
【答案】
(1)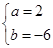
(2)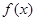 在
在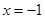 处有极大值
处有极大值 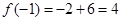 无极小值.
无极小值.
【解析】
试题分析:∵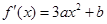
(1)∴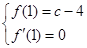 ∴
∴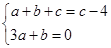 ∴
∴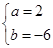
(2)因为其为奇函数∴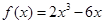 ∴
∴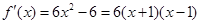
令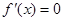 ∴
∴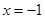 或1 ∵
或1 ∵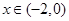 ∴
∴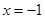
∴当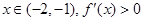
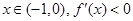
∴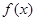 在
在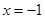 处有极大值
处有极大值 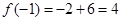 无极小值.
无极小值.
考点:本题主要考查应用导数研究函数的单调性、极值。
点评:中档题,本题属于导数应用中的基本问题,通过研究导数的正负,明确函数的单调性。判断函数的驻点是何种类型的极值点。

练习册系列答案
相关题目
 在
在 处取得极值.
处取得极值. ;
; ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围. =
= 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 在
在 处取得极值。
处取得极值。 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 为实数。
为实数。 在
在 处取得极值,求
处取得极值,求 的值;
的值;
 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。 在
在 处取得极值.
处取得极值. 的值;[来源:学+科+网]
的值;[来源:学+科+网] 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围.
的取值范围.