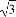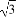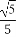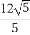Question

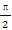在△ABC中,A,B,C为三个内角,a,b,c为三条边,<C<且=.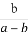

(1)判断△ABC的形状.

(2)若|+|=2,求·的取值范围.

 

Answer 1

(1) △ABC为等腰三角形 (2) (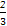,1)

【解析】(1)由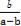=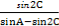及正弦定理有:

sinB=sin 2C,

∴B=2C或B+2C=π.

若B=2C,且<C<,

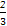∴π<B<π,B+C>π(舍).

∴B+2C=π,则A=C,

∴△ABC为等腰三角形.

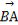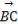(2)∵|+|=2,

∴a2+c2+2ac·cosB=4,

∵a=c,∴cosB=,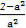

而cosB=-cos 2C,

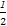∴<cosB<1,

∴1<a2<,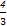

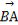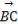∴·=2-a2,

故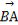·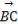∈(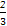,1).