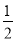Question

已知函数y＝f(x)是R上的偶函数，对?x∈R都有f(x＋4)＝f(x)＋f(2)成立．当x1，x2∈[0,2]，且x1≠x2时，都有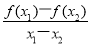<0，给出下列命题：

①f(2)＝0；

②直线x＝－4是函数y＝f(x)图象的一条对称轴；

③函数y＝f(x)在[－4,4]上有四个零点；

④f(2 014)＝0.

其中所有正确命题的序号为________．

 

Answer 1

①②④

【解析】令x＝－2，得f(－2＋4)＝f(－2)＋f(2)，解得f(－2)＝0，因为函数f(x)为偶函数，所以f(2)＝0，①正确；因为f(－4＋x)＝f(－4＋x＋4)＝f(x)，f(－4－x)＝f(－4－x＋4)＝f(－x)＝f(x)，所以f(－4＋x)＝f(－4－x)，即x＝－4是函数f(x)的一条对称轴，②正确；当x1，x2∈[0,2]，且x1≠x2时，都有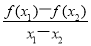<0，说明函数f(x)在[0,2]上是单调递减函数，又f(2)＝0，因此函数f(x)在[0,2]上只有一个零点，由偶函数知函数f(x)在[－2,0]上也只有一个零点，由f(x＋4)＝f(x)，知函数的周期为4，所以有函数f(x)在(2,6]与[－6，－2]上也单调且有f(6)＝f(－6)＝0，因此，函数在[－4,4]上只有2个零点，③错；对于④，因为函数的周期为4，即有f(2)＝f(6)＝f(10)＝…＝f(2 014)＝0，④正确．