题目内容
一个口袋中装有大小和质地都相同的白球和红球共7个,其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)=
.
(1)求口袋中的白球个数;
(2)求X的概率分布与数学期望.
| 2 | 7 |
(1)求口袋中的白球个数;
(2)求X的概率分布与数学期望.
分析:(1)设口袋中白球数为n,根据P(X=2)=
建立等式,解之即可求出所求;
(2)X的取值可能为1,2,3,4,然后根据等可能事件的概率公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
| 2 |
| 7 |
(2)X的取值可能为1,2,3,4,然后根据等可能事件的概率公式求出相应的概率,列出分布列,最后根据数学期望公式解之即可.
解答:解:(1)设口袋中白球数为n,则由P(X=2)=
得:
=
即n(7-n)=12解得n=4或3
因为白球数不少于红球数,故白球个数为4个
(2)因为X的取值可能为1,2,3,4;
P(X=1)=
=
,P(X=2)=
P(X=3)=
=
,P(X=4)=
=
所以X的分布列为
∴E(x)=1×
+2×
+3×
+4×
=1.6
即X的数学期望为1.6
| 2 |
| 7 |
得:
| ||||
|
| 2 |
| 7 |
即n(7-n)=12解得n=4或3
因为白球数不少于红球数,故白球个数为4个
(2)因为X的取值可能为1,2,3,4;
P(X=1)=
| ||
|
| 4 |
| 7 |
| 2 |
| 7 |
P(X=3)=
| ||||
|
| 4 |
| 35 |
| ||||
|
| 1 |
| 35 |
所以X的分布列为
| X | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 4 |
| 7 |
| 2 |
| 7 |
| 4 |
| 35 |
| 1 |
| 35 |
即X的数学期望为1.6
点评:本题主要考查了离散型随机变量的期望,以及离散型随机变量及其分布列,同时考查了等可能事件的概率和计算能力,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
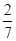 .
. .
. .
.