题目内容
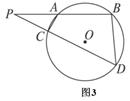
如图，PAB，PCD是圆的两条割线，BC交AD于E，连接BD、AC，则图中的相似三角形有（ ）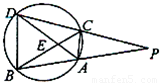
A．2对
B．3对
C．4对
D．5对
【答案】分析：根据圆内的一条弦所对的圆周角相等，即可求得三角形相似，分别计算相似三角形的对数，即可解题．
解答：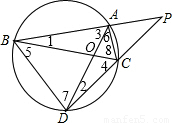
解：如图，∵∠5、∠6为CD所对的圆周角，∠7、∠8为AB所对的圆周角，
∴∠5=∠6，∠7=∠8，
∴△ACO∽△BDO
∵∠2、∠1为AC所对的圆周角，∠P=∠P，
∴△APD∽△CPB．
∵∠3、∠4为BD所对的圆周角，
∴∠3=∠4，
∵∠1=∠2，
∴△ABO∽△CDO．
∵∠1+∠5=∠PBD，∠ACP=∠2+∠6，∠1=∠2，∠5=∠6，
∴△PAC∽△PDB．
共有4对．
故选C．
点评：本题考查了弦所对的圆周角相等的性质，相似三角形的证明，本题中根据一条弦所对的圆周角相等求证三角形相似是解题的关键．
解答：
解：如图，∵∠5、∠6为CD所对的圆周角，∠7、∠8为AB所对的圆周角，∴∠5=∠6，∠7=∠8，
∴△ACO∽△BDO
∵∠2、∠1为AC所对的圆周角，∠P=∠P，
∴△APD∽△CPB．
∵∠3、∠4为BD所对的圆周角，
∴∠3=∠4，
∵∠1=∠2，
∴△ABO∽△CDO．
∵∠1+∠5=∠PBD，∠ACP=∠2+∠6，∠1=∠2，∠5=∠6，
∴△PAC∽△PDB．
共有4对．
故选C．
点评：本题考查了弦所对的圆周角相等的性质，相似三角形的证明，本题中根据一条弦所对的圆周角相等求证三角形相似是解题的关键．
练习册系列答案
相关题目
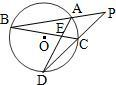9、如图，PAB、PCD为⊙O的两条割线，AD、BC相交于点E，则图中相似三角形共有（ ）
（几何证明选讲选做题）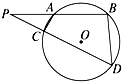
（2012•肇庆一模）（几何证明选讲选做题）如图，PAB、PCD为⊙O的两条割线，若 PA=5，AB=7，CD=11，AC=2，则BD等于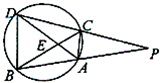
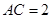，则BD等于
