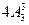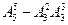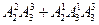题目内容
设直线方程为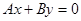 ,从1,2,3,4,5中每次取两个不同的数作为
,从1,2,3,4,5中每次取两个不同的数作为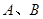 的值,则所得不同直线的条数为
的值,则所得不同直线的条数为
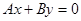 ,从1,2,3,4,5中每次取两个不同的数作为
,从1,2,3,4,5中每次取两个不同的数作为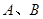 的值,则所得不同直线的条数为
的值,则所得不同直线的条数为 | A.20 | B.19 | C.18 | D.16 |
C
分析:利用计数原理,从5个数取2个不同的数可用公式c52算出,然后考虑到A与B的比值相等时直线重合,把重合的情况除过即可得到不同直线的条数.
解:从1,2,3,4,5这五个数中每次取两个不同的数作为A、B的值,取法数为A52,
而当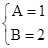 与
与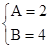 ;
; 与
与
时所得直线重合,
则所得不同直线为A52-2=5×4-2=18(条)
故选C
点评:考查学生会利用计数原理解决数学问题,掌握直线重合时满足的条件.
解:从1,2,3,4,5这五个数中每次取两个不同的数作为A、B的值,取法数为A52,
而当
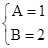 与
与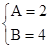 ;
; 与
与
则所得不同直线为A52-2=5×4-2=18(条)
故选C
点评:考查学生会利用计数原理解决数学问题,掌握直线重合时满足的条件.

练习册系列答案
相关题目
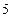 名男生、
名男生、 名女生站成一排照相.(用数字作答)
名女生站成一排照相.(用数字作答)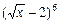 的展开式中x2的系数为 .(用数字作答)
的展开式中x2的系数为 .(用数字作答) 数有( )
数有( )