题目内容
设U=R,集合A={x|x<-3或x>3},B=(-∞,1)∪(4,+∞),则(C∪A)∪B=
(-∞,3]∪(4,+∞)
(-∞,3]∪(4,+∞)
.分析:先由全集U=R,求A的补集C∪A,接着利用画数轴求出(C∪A)∪B即可.
解答:解:∵U=R,集合A={x|x<-3或x>3},
∴C∪A={x|-3≤x≤3}.
∵B=(-∞,1)∪(4,+∞),
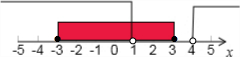
∴集合(C∪A)∪B=(-∞,3]∪(4,+∞),
故答案为:(-∞,3]∪(4,+∞).
∴C∪A={x|-3≤x≤3}.
∵B=(-∞,1)∪(4,+∞),

∴集合(C∪A)∪B=(-∞,3]∪(4,+∞),
故答案为:(-∞,3]∪(4,+∞).
点评:本题属于以不等式为依托,求集合的并集补集的基础题,也是高考常会考的基本题型.

练习册系列答案
相关题目
设U=R,集合A={y|y=
,x≥1},B={x∈Z|x2-4≤0},则下列结论正确的是( )
| x-1 |
| A、A∩B={-2,-1} |
| B、(?UA)∪B=(-∞,0) |
| C、A∪B=[0,+∞) |
| D、(?UA)∩B={-2,-1} |