题目内容
设有两个二次方程,他们分别是x2+2ax+1=0和ax2+ax+1=0.已知这两个方程中至少有一个有实数解,求实数a的取值范围.分析:法一:由这两个方程中至少有一个有实数解,可得这两个方程有解,一元二次方程有解可得出判别式△≥0,由此不等式的求出a的两个取值范围,然后求并集;
法二:至少有一个有实数解的反面就是两个都无解,一元二次方程无解可得出判别式△<0,由此不等式的求出a的取值范围,两范围取交集,这个集合的补集就是要求的a的取值范围.
法二:至少有一个有实数解的反面就是两个都无解,一元二次方程无解可得出判别式△<0,由此不等式的求出a的取值范围,两范围取交集,这个集合的补集就是要求的a的取值范围.
解答:解:(法一)方程x2+2ax+1=0有实数解⇒△1=4a2-4≥0(4分)
⇒a≤-1或a≥1(5分)
方程ax2+ax+1=0有实数解⇒
(9分)
⇒a<0或a≥4(10分)
所以,所求实数a的取值范围是(-∞,0)∪[1,+∞)(14分)
(法二)方程x2+2ax+1=0和ax2+ax+1=0均无实数解⇒
(8分)
⇒0<a<1(10分)
则两个方程中至少有一个有实数解⇒a≤0或a≥1(12分)
又a≠0,所以,所求实数a的取值范围是(-∞,0)∪[1,+∞)(14分)
⇒a≤-1或a≥1(5分)
方程ax2+ax+1=0有实数解⇒
|
⇒a<0或a≥4(10分)
所以,所求实数a的取值范围是(-∞,0)∪[1,+∞)(14分)
(法二)方程x2+2ax+1=0和ax2+ax+1=0均无实数解⇒
|
⇒0<a<1(10分)
则两个方程中至少有一个有实数解⇒a≤0或a≥1(12分)
又a≠0,所以,所求实数a的取值范围是(-∞,0)∪[1,+∞)(14分)
点评:本题主要考查一元二次方程的分布与系数的关系,注意“至少有一个”,故可以从反面考虑.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,
 对于定义域内的
对于定义域内的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 有两个极值点
有两个极值点 ,
, 且
且 ,求证:
,求证: ;
; 若对任意的
若对任意的 ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.  (a
> 0,且a ≠ 1)的解集是{ x | x < 0 };
(a
> 0,且a ≠ 1)的解集是{ x | x < 0 }; 的定义域为R.如果
的定义域为R.如果 为真命题,
为真命题, 为假命题,
为假命题,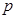 :关于
:关于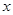 的不等式
的不等式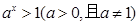 的解集是
的解集是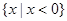 ;
;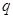 :函数
:函数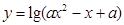 的定义域为R,如果
的定义域为R,如果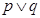 为真命题,
为真命题,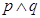 为假命题,求实数
为假命题,求实数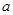 的取值范围。
的取值范围。