题目内容
选修4-2：矩阵与变换已知矩阵
，
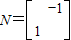．在平面直角坐标系中，设直线2x-y+1=0在矩阵MN对应的变换作用下得到曲线F，求曲线F的方程．
【答案】分析：先求MN，再利用点（x，y）在矩阵MN对应的变换作用下变为（x′，y′），得出坐标之间的关系，利用点（x，y）在直线2x-y+1=0上，即可求得曲线F的方程．
解答：解：由题设得MN=
．…（3分）
设（x，y）是直线2x-y+1=0上任意一点，点（x，y）在矩阵MN对应的变换作用下变为（x′，y′），
则有
=
，即
，所以
…（7分）
因为点（x，y）在直线2x-y+1=0上，从而2x′-（-y′）+1=0，
即2x′+y′+1=0．
所以曲线F的方程为2x+y+1=0． …（10分）
点评：本题考查矩阵变换，考查矩阵的乘法，考查代入法求曲线的方程，属于基础题．
解答：解：由题设得MN=
．…（3分）设（x，y）是直线2x-y+1=0上任意一点，点（x，y）在矩阵MN对应的变换作用下变为（x′，y′），
则有
=，即，所以…（7分）因为点（x，y）在直线2x-y+1=0上，从而2x′-（-y′）+1=0，
即2x′+y′+1=0．
所以曲线F的方程为2x+y+1=0． …（10分）
点评：本题考查矩阵变换，考查矩阵的乘法，考查代入法求曲线的方程，属于基础题．
练习册系列答案
相关题目
是将平面上每个点
的横坐标乘
，纵坐标乘
，变到点
.
在变换
的极坐标方程为：
，直线
的参数方程为：
（
为参数）.
，曲线
的值．
为实数，且
．
为参数），C2的参数方程为
为参数）
的定义域为R，求实数m的取值范围．
是将平面上每个点
的横坐标乘
，纵坐标乘
，变到点
.
在变换
的极坐标方程为：
，直线
的参数方程为：
（
为参数）.
，曲线
的值．
为实数，且
