题目内容
已知函数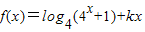 (k∈R)是偶函数.
(k∈R)是偶函数.(1)求k的值;
(2)定理:函数
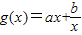 (a、b是正常数)在区间
(a、b是正常数)在区间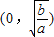 上为减函数,在区间
上为减函数,在区间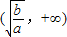 上为增函数.参考该定理,解决下面问题:是否存在实数m同时满足以下两个条件:①不等式
上为增函数.参考该定理,解决下面问题:是否存在实数m同时满足以下两个条件:①不等式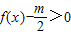 恒成立;②方程f(x)-m=0有解.若存在,试求出实数m的取值范围,若不存在,请说明理由.
恒成立;②方程f(x)-m=0有解.若存在,试求出实数m的取值范围,若不存在,请说明理由.
【答案】分析:(1)根据函数f(x)是偶函数建立等式关系,化简可得log4 =-2kx,从而x=-2kx对x∈R恒成立,即可求出k的值;
=-2kx,从而x=-2kx对x∈R恒成立,即可求出k的值;
(2)先利用①不等式 恒成立等价于
恒成立等价于 ,建立不等关系求出m的范围,再根据②要使方程f(x)-m=0有解,转化成求函数的值域,将m分离出来得m=log4
,建立不等关系求出m的范围,再根据②要使方程f(x)-m=0有解,转化成求函数的值域,将m分离出来得m=log4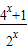 =log4(2x+
=log4(2x+ ),然后利用所给定理求出m的范围,最后综合即可.
),然后利用所给定理求出m的范围,最后综合即可.
解答:解:(1)由函数f(x)是偶函数,可知f(x)=f(-x).
∴log4(4x+1)+kx=log4(4-x+1)-kx.…(2分)
即log4 =-2kx,log44x=-2kx,…(4分)
=-2kx,log44x=-2kx,…(4分)
∴x=-2kx对一切x∈R恒成立.∴k=- .…(6分)
.…(6分)
(利用f(-1)=f(1)解出k=- ,可得满分)
,可得满分)
(2)由m=f(x)=log4(4x+1)- x,
x,
∴m=log4 =log4(2x+
=log4(2x+ ).…(8分)
).…(8分)
设u=2x+ ,又设t=2x,则
,又设t=2x,则 ,由定理,知umin=u(1)=2,…(10分)
,由定理,知umin=u(1)=2,…(10分)
∴m≥log42= .故要使方程f(x)-m=0有解,m的取值范围为m≥
.故要使方程f(x)-m=0有解,m的取值范围为m≥ .…(12分)
.…(12分)

 ,
,
∴ ,
,
综上所述, …(14分)
…(14分)
点评:本题主要考查了函数奇偶性的应用,以及根的个数的判定和利用新定理等有关基础知识,属于中档题.
 =-2kx,从而x=-2kx对x∈R恒成立,即可求出k的值;
=-2kx,从而x=-2kx对x∈R恒成立,即可求出k的值;(2)先利用①不等式
 恒成立等价于
恒成立等价于 ,建立不等关系求出m的范围,再根据②要使方程f(x)-m=0有解,转化成求函数的值域,将m分离出来得m=log4
,建立不等关系求出m的范围,再根据②要使方程f(x)-m=0有解,转化成求函数的值域,将m分离出来得m=log4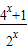 =log4(2x+
=log4(2x+ ),然后利用所给定理求出m的范围,最后综合即可.
),然后利用所给定理求出m的范围,最后综合即可.解答:解:(1)由函数f(x)是偶函数,可知f(x)=f(-x).
∴log4(4x+1)+kx=log4(4-x+1)-kx.…(2分)
即log4
 =-2kx,log44x=-2kx,…(4分)
=-2kx,log44x=-2kx,…(4分)∴x=-2kx对一切x∈R恒成立.∴k=-
 .…(6分)
.…(6分)(利用f(-1)=f(1)解出k=-
 ,可得满分)
,可得满分)(2)由m=f(x)=log4(4x+1)-
 x,
x,∴m=log4
 =log4(2x+
=log4(2x+ ).…(8分)
).…(8分)设u=2x+
 ,又设t=2x,则
,又设t=2x,则 ,由定理,知umin=u(1)=2,…(10分)
,由定理,知umin=u(1)=2,…(10分)∴m≥log42=
 .故要使方程f(x)-m=0有解,m的取值范围为m≥
.故要使方程f(x)-m=0有解,m的取值范围为m≥ .…(12分)
.…(12分)
 ,
,∴
 ,
,综上所述,
 …(14分)
…(14分)点评:本题主要考查了函数奇偶性的应用,以及根的个数的判定和利用新定理等有关基础知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (k∈R),若函数
(k∈R),若函数 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( ) (k∈R).
(k∈R).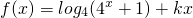 (k∈R)是偶函数.
(k∈R)是偶函数.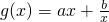 (a、b是正常数)在区间
(a、b是正常数)在区间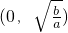 上为减函数,在区间
上为减函数,在区间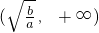 上为增函数.参考该定理,解决下面问题:是否存在实数m同时满足以下两个条件:①不等式
上为增函数.参考该定理,解决下面问题:是否存在实数m同时满足以下两个条件:①不等式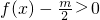 恒成立;②方程f(x)-m=0有解.若存在,试求出实数m的取值范围,若不存在,请说明理由.
恒成立;②方程f(x)-m=0有解.若存在,试求出实数m的取值范围,若不存在,请说明理由. (k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
(k∈R),若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )