题目内容
已知正三角形AOB的顶点A,B在抛物线 上,O为坐标原点,则
上,O为坐标原点,则 ( )
( )
A. | B. | C. | D. |
C
解析试题分析:设其中一个顶点是(x,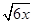 )因为是正三角形,所以
)因为是正三角形,所以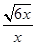 =tan30°=
=tan30°=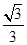
即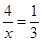 解得x=12,所以另外两个顶点是(12,3
解得x=12,所以另外两个顶点是(12,3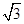 )与(12,-3
)与(12,-3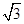 )
)
三角形的面积12•(3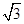 +3
+3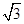 )•
)•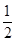 =36
=36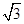 ,故选C
,故选C
考点:本题主要考查了抛物线的应用.利用抛物线性质解决解三角形问题.
点评:解决该试题的关键是根据抛物线方程先设其中一个顶点是(x,2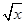 ),根据正三角形的性质, tan30°=
),根据正三角形的性质, tan30°=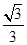 ,进而利用三角形的性质得到结论。
,进而利用三角形的性质得到结论。

练习册系列答案
相关题目
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积( )
| A.9 | B.9 | C.18 | D. |
在 中,若
中,若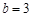 ,
, ,
, ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
在 中,角
中,角 的对边分别为
的对边分别为 若
若 若
若 有两解,则
有两解,则 的范围是( )
的范围是( )
| A.(1,2) | B.(2,3) | C.(2, ) ) | D.(4, ) ) |
在△ 中,若
中,若 ,则△
,则△ 的形状是
的形状是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |
甲船在岛B的正南方A处,AB=10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
| A.21.5分钟 | B. 分钟 分钟 | C. 分钟 分钟 | D.2.15分钟 |
在  中,角C为最大角,且
中,角C为最大角,且 ,则
,则 是
是
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.形状不确定 |
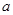 、b、c。若
、b、c。若 ,则
,则


 ,那么cosC等于 ( )
,那么cosC等于 ( )


