题目内容
(本小题满分12分)
已知 ,其中向量
,其中向量 , (
, ( R).
R).
(1)
求 的最小正周期和最小值;
的最小正周期和最小值;
(2)
在△ABC中,角A、B、C的对边分别为 、
、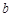 、
、 ,若
,若 ,a=2
,a=2 ,
, ,求边长
,求边长 的值.
的值.
【答案】
(1) f(x)的最小正周期为π,最小值为-2.(2) c=2或c=6。
【解析】
试题分析:(1)
f(x)=a·b-1=(sin2x,2cosx)·(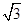 ,cosx)-1
,cosx)-1
=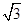 sin2
x +2cos2 x -1=
sin2
x +2cos2 x -1=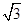 sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+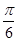 ) 4分
) 4分
∴f(x)的最小正周期为π,最小值为-2. 6分
(2) f(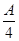 )=2sin(
)=2sin(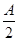 +
+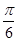 )=
)=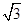
∴sin(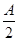 +
+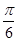 )=
)=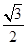 8分
8分
∴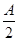 +
+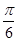 =
=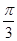 ∴
A=
∴
A=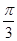 或
或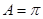 (舍去) 10分
(舍去) 10分
由余弦定理得a2=b2+c2-2bccosA
52=64+c2-8c即c2-8c+12="0"
从而c=2或c=6 12分
考点:本题主要考查平面向量的坐标运算,三角函数和差倍半公式,三角函数性质,余弦定理的应用。
点评:典型题,为研究三角函数的图象和性质,往往需要利用三角函数和差倍半公式将函数“化一”。本题由平面向量的坐标运算得到f(x)的表达式,通过“化一”,利用三角函数性质,求得周期、最小值。(2)则利用余弦定理,得到c的方程,达到解题目的。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目