题目内容
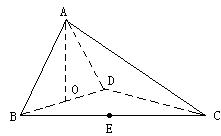
(19)如图,四面体ABCD中,O、E分别是BD、BC的中点, ![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
本小题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离基本知识,考查空间想象能力、逻辑思维能力和运算能力。
方法一:
(I)证明:连结OC
![]()
![]()
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]()
![]()
![]() 平面
平面![]()
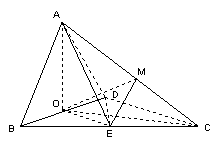
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在![]() 中,
中,
![]()
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,![]()
![]()
![]() 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为![]()
(III)解:设点E到平面ACD的距离为![]()
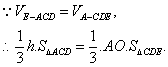
在![]() 中,
中,![]()
![]()
而![]()
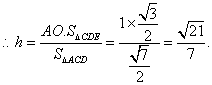
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]()
方法二:
(I)同方法一。
(II)解:以O为原点,如图建立空间直角坐标系,则![]()
![]()
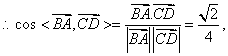
![]() 异面直线AB与CD所成角
异面直线AB与CD所成角
的大小为![]()
(III)解:设平面ACD的法向量为![]() 则
则
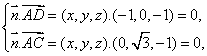
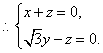
令![]() 得
得![]() 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
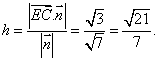

(12分)19.(本题满分12分)
如图,已知四面体ABCD中, .
.
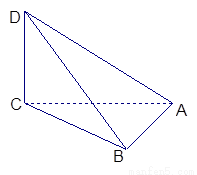
(1)指出与面BCD垂直的面,并加以证明.
(2)若AB=BC=1,CD= ,二面角C-AD-B的平面角为
,二面角C-AD-B的平面角为 ,
, ,求
,求 的表达式及其取值范围.
的表达式及其取值范围.
19
|
|
|
|
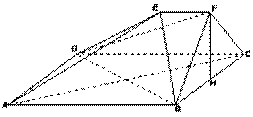 如图,在多面体ABCDEF中,ABCD是正方形,AB=2EF=2,
如图,在多面体ABCDEF中,ABCD是正方形,AB=2EF=2,![]() ,EF⊥FB,∠BFC=
,EF⊥FB,∠BFC=![]() ,BF=FC,H为BC的中点.
,BF=FC,H为BC的中点.
(Ⅰ)求证:![]() 平面EDB;
平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积.