题目内容
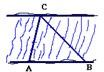 如图某河段的两岸可视为平行,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=200米.则A、C两点的距离为( )
如图某河段的两岸可视为平行,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=200米.则A、C两点的距离为( )A、
| ||||
B、100
| ||||
C、
| ||||
D、200
|
分析:先通过三角形内角和为180°及∠CAB=75°,∠CBA=45°可求出∠ACB,进而通过正弦定理求出AC.
解答:解:∵∠CAB=75°,∠CBA=45°,
∴∠ACB=180°-∠CAB-∠CBA=180°-75°-45°=60°
根据正弦定理
=
∴AC=
•sinB=
×
=
故选A
∴∠ACB=180°-∠CAB-∠CBA=180°-75°-45°=60°
根据正弦定理
| AC |
| sinB |
| AB |
| sinC |
∴AC=
| AB |
| sinC |
| 200 | ||||
|
| ||
| 2 |
200
| ||
| 3 |
故选A
点评:本题主要考查正弦定理的应用.作为解决三角形边角问题的常用方法,我们应重点掌握.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
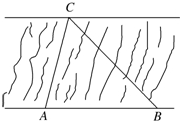 如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=100米.
如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,且AB=100米. ,
, ,且
,且 米.
米.
 ;
; ,观察对岸的点
,观察对岸的点 ,测得
,测得
 ,且
,且 米.
米. ;
;
 ,
, ,且
,且 米。
米。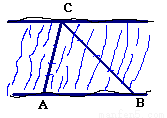
 ;
;