题目内容
已知函数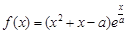 (
(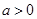 ).
).
(1)当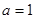 时,求函数
时,求函数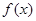 的单调区间;
的单调区间;
(2)当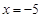 时,
时,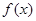 取得极值,求函数
取得极值,求函数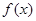 在
在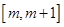
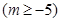 上的最小值;
上的最小值;
【答案】
(1)单调增区间为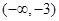 和
和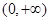 ,单调减区间为
,单调减区间为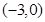 ;
;
(2)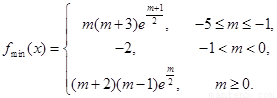 .
.
【解析】
试题分析:(1)求导解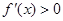 得
得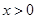 或
或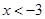 , 解
, 解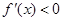 得
得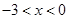 ;
;
(2)当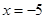 时,
时,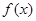 取得极值, 所以
取得极值, 所以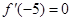 解得
解得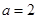 ,对
,对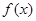 求导,判断在
求导,判断在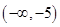 ,
,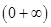 递增,在
递增,在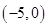 递减,分类讨论,求出最小值.
递减,分类讨论,求出最小值.
试题解析:(1)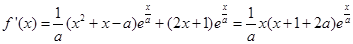
当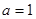 时,
时,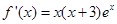
解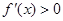 得
得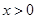 或
或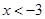 , 解
, 解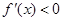 得
得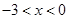
所以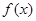 单调增区间为
单调增区间为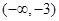 和
和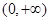 ,单调减区间为
,单调减区间为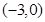
(2)当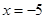 时,
时,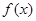 取得极值, 所以
取得极值, 所以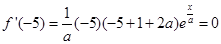
解得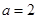 (经检验
(经检验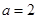 符合题意)
符合题意)
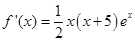
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
↘ |
|
↗ |
所以函数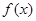 在
在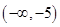 ,
,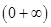 递增,在
递增,在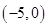 递减
递减
当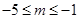 时,
时,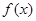 在
在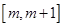 单调递减,
单调递减,
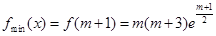
当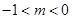 时
时 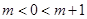
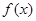 在
在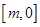 单调递减,在
单调递减,在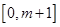 单调递增,
单调递增,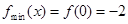
当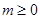 时,
时,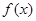 在
在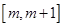 单调递增,
单调递增,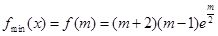
综上,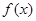 在
在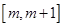 上的最小值
上的最小值
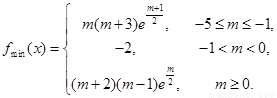 .
.
考点:求导判断函数单调性,求函数最值.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
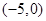
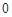
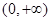
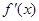
 ↗
↗