题目内容
如果2+i是关于x的实系数方程x2+mx+n=0的一个根,则圆锥曲线
+
=1的焦点坐标是( )
| x2 |
| m |
| y2 |
| n |
| A、(±1,0) |
| B、(0,±1) |
| C、(±3,0) |
| D、(0,±3) |
分析:由2+i是关于x的实系数方程x2+mx+n=0的一个根,知(2+i)2+m(2+i)+n=0,由此能得到m=-4,n=5.故圆锥曲线为
-
=1,由此能求出其焦点坐标.
| y2 |
| 5 |
| x2 |
| 4 |
解答:解:∵2+i是关于x的实系数方程x2+mx+n=0的一个根,
∴(2+i)2+m(2+i)+n=0,
∴
,
∴m=-4,n=5.
∴圆锥曲线
+
=1为
-
=1,
故其焦点坐标为(0,±3).
故选D.
∴(2+i)2+m(2+i)+n=0,
∴
|
∴m=-4,n=5.
∴圆锥曲线
| x2 |
| m |
| y2 |
| n |
| y2 |
| 5 |
| x2 |
| 4 |
故其焦点坐标为(0,±3).
故选D.
点评:本题考查椭圆的基本性质和应用,解题时要注意复数相等的概念的合理运用.

练习册系列答案
相关题目
 的焦点坐标是( )
的焦点坐标是( ) 的焦点坐标是( )
的焦点坐标是( )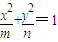 的焦点坐标是( )
的焦点坐标是( ) 的焦点坐标是( )
的焦点坐标是( )