题目内容
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为| ? |
| y |
①y与x具有正的线性相关关系;
②回归直线过样本点的中心(
. |
| x |
. |
| y |
③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是
分析:根据回归方程为
=0.85x-85.71,0.85>0,可知①②③均正确,对于④回归方程只能进行预测,但不可断定.
| ? |
| y |
解答:解:对于①,0.85>0,所以y与x具有正的线性相关关系,故正确;
对于②,回归直线过样本点的中心(
,
),故正确;
对于③,∵回归方程为
=0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于④,x=170cm时,
═0.85×170-85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确.
故答案为:①②③.
对于②,回归直线过样本点的中心(
. |
| x |
. |
| y |
对于③,∵回归方程为
| ? |
| y |
对于④,x=170cm时,
| ? |
| y |
故答案为:①②③.
点评:本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.

练习册系列答案
相关题目

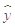 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )  ,
,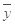 )
) =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是 ,
,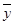 )
) =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是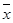 ,
,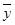 )
)