题目内容
已知二次函数f（x）=﹣3x2+2bx+c的图象经过原点，其对称轴方程为x=2．
（1）求函数f（x）的解析式；
（2）当x∈[2，3]时，求函数g（x）=f（x）﹣6（m+2）x﹣9的最大值h（m）．
（1）求函数f（x）的解析式；
（2）当x∈[2，3]时，求函数g（x）=f（x）﹣6（m+2）x﹣9的最大值h（m）．
解：（1）二次函数f（x）=﹣3x2+2bx+c的图象经过原点，则c=0，
又∵二次函数的图象对称轴是直线x=2，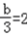
，
∴二次函数解析式为：y=﹣3x2+12x．
（2）g（x）=f（x）﹣6（m+2）x﹣9=﹣3x2﹣6mx﹣9，x∈[2，3]．
配方得，g（x）=﹣3（x+m）2+3m2﹣9，
∵m∈[﹣3，+∞），
∴﹣m∈（﹣∞，3]
①当﹣m＜2时，m＞﹣2时，h（m）=g（2）=﹣12m﹣21；
②当2≤﹣m≤3时，﹣3≤m≤﹣2时，h（m）=g（﹣m）=3m2﹣9．
③当﹣m＞3时，m＜﹣3时，h（m）=g（3）=﹣36﹣18m．
综上，h（m）=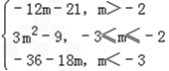
．
又∵二次函数的图象对称轴是直线x=2，
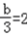， ∴二次函数解析式为：y=﹣3x2+12x．
（2）g（x）=f（x）﹣6（m+2）x﹣9=﹣3x2﹣6mx﹣9，x∈[2，3]．
配方得，g（x）=﹣3（x+m）2+3m2﹣9，
∵m∈[﹣3，+∞），
∴﹣m∈（﹣∞，3]
①当﹣m＜2时，m＞﹣2时，h（m）=g（2）=﹣12m﹣21；
②当2≤﹣m≤3时，﹣3≤m≤﹣2时，h（m）=g（﹣m）=3m2﹣9．
③当﹣m＞3时，m＜﹣3时，h（m）=g（3）=﹣36﹣18m．
综上，h（m）=
．
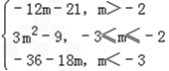练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目