题目内容
已知向量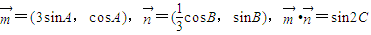 ,且A、B、C分别为△ABC三边a、b、c所对的角.
,且A、B、C分别为△ABC三边a、b、c所对的角.(Ⅰ)求角C的大小;
(Ⅱ)若sinA,sinB,sinC成等比数列,且
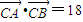 ,求c的值.
,求c的值.
【答案】分析:(1)首先由题意得到sinAcosB+cosAsinB=sin2C,由sin[180°-(A+B)]=sinC得出sinC=sin2C,进而得到cosC= ,从而求出角C的度数;
,从而求出角C的度数;
(2)根据等差数列性质,得出sin2C=sinAsinB,进而求正弦定理得到c2=ab,由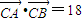 能够求得ab=36,即可求出c的值.
能够求得ab=36,即可求出c的值.
解答:解:(Ⅰ)∵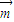 =(3sinA,cosA),
=(3sinA,cosA), =
=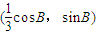 ,
,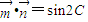
∴sinAcosB+cosAsinB=sin2C即sinC=sin2C(3分)
∵sinC≠0∴cosC= 又C为三角形的内角,∴
又C为三角形的内角,∴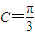 (5分)
(5分)
(Ⅱ)∵sinA,sinC,sinB成等比数列,∴sin2C=sinAsinB(6分)
∴c2=ab又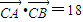 (7分)
(7分)
∴abcosC=18(8分)
∴ab=36故c2=36∴c=6(10分)
点评:本题考查了三角函数化简求值、等比数列的性质以及正弦定理等知识,在三角形中尤其要注意内角和180°的灵活运用.属于基础题.
 ,从而求出角C的度数;
,从而求出角C的度数;(2)根据等差数列性质,得出sin2C=sinAsinB,进而求正弦定理得到c2=ab,由
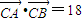 能够求得ab=36,即可求出c的值.
能够求得ab=36,即可求出c的值.解答:解:(Ⅰ)∵
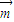 =(3sinA,cosA),
=(3sinA,cosA), =
=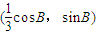 ,
,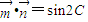
∴sinAcosB+cosAsinB=sin2C即sinC=sin2C(3分)
∵sinC≠0∴cosC=
 又C为三角形的内角,∴
又C为三角形的内角,∴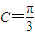 (5分)
(5分)(Ⅱ)∵sinA,sinC,sinB成等比数列,∴sin2C=sinAsinB(6分)
∴c2=ab又
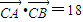 (7分)
(7分)∴abcosC=18(8分)
∴ab=36故c2=36∴c=6(10分)
点评:本题考查了三角函数化简求值、等比数列的性质以及正弦定理等知识,在三角形中尤其要注意内角和180°的灵活运用.属于基础题.

练习册系列答案
相关题目
 ,且A、B、C三点共线,
,且A、B、C三点共线, ,且A、B、C分别为
,且A、B、C分别为 的三边a、b、c所对的角。
的三边a、b、c所对的角。 求c边的长。
求c边的长。 ,且A,B,C分别是△ABC三边a,b,c所对的角.
,且A,B,C分别是△ABC三边a,b,c所对的角. ,求c的值.
,求c的值. ,且A,B,C分别是△ABC三边a,b,c所对的角.
,且A,B,C分别是△ABC三边a,b,c所对的角. ,求c的值.
,求c的值.