题目内容
设A=lg（x2+2），B=lg（2x），则A与B的大小关系是（ ）
| A．A≥B | B．A＜B | C．A=B | D．A＞B |
∵A=lg（x2+2），B=lg（2x），
∴2x＞0，即x＞0，
∵x2+2=x2+1+1≥2
+1=2x+1＞2x，
又∵函数y=lgx是（0，+∞）上的单调递增函数，
∴lg（x2+2）＞lg（2x），
即A＞B．
故选：D．
∴2x＞0，即x＞0，
∵x2+2=x2+1+1≥2
| x2•1 |
又∵函数y=lgx是（0，+∞）上的单调递增函数，
∴lg（x2+2）＞lg（2x），
即A＞B．
故选：D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
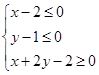表示的平面区域上运动，则x－y的取值范围是( ).