题目内容
设CD是△ABC的边AB上的高,且满足
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
分析:根据三角函数的定义先求出
=sinA,
=sinB,再由sin2A=1-sin2B=cos2B,分sinA=cosB 和 sinA=-cosB,利用诱导公式可得答案.
| CD |
| AC |
| CD |
| BC |
解答:解:由题意可得,
=sinA,
=sinB,
+
=1,
∴sin2A+sin2B=1,即sin2A=1-sin2B=cos2B.
故有 sinA=cosB,或sinA=-cosB,
①若sinA=cosB,则有sinA=sin(π-A)=sin(
-B),∴A=
-B,或 π-A=
-B,解得 A+B=
或 A-B=
.
②若sinA=-cosB,则B为钝角,A为锐角,故有 sinA=cos(π-B)=sin[
-(π-B)]=sin(B-
),则有 A=B-
,即 B-A=
.
综合①②可得,A+B=
、或 A-B=
、或 B-A=
,
故选D.
| CD |
| AC |
| CD |
| BC |
| CD2 |
| AC2 |
| CD2 |
| BC2 |
∴sin2A+sin2B=1,即sin2A=1-sin2B=cos2B.
故有 sinA=cosB,或sinA=-cosB,
①若sinA=cosB,则有sinA=sin(π-A)=sin(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
②若sinA=-cosB,则B为钝角,A为锐角,故有 sinA=cos(π-B)=sin[
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
综合①②可得,A+B=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选D.
点评:本题主要考查三角函数的定义,这里注意三角函数的取值,尤其是在三角形中角的变化范围,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则( )
,则( )  B.
B.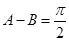
 D.
D.
 ,则( )
,则( )
 或
或
 或
或
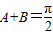 或
或
 ,则( )
,则( )
 或
或
 或
或
 或
或