题目内容
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为 ,现随机从中抽取2人上台抽奖,
,现随机从中抽取2人上台抽奖,
求 和
和 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
(1)160;(2)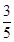 ;(3)
;(3)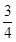
解析试题分析:(1)分层抽样是安比例抽取,所以根据比例相等列式计算。(2)属古典概型概率,用例举法将所有情况一一例举出来计算基本事件总数,再将符合要求的事件找出来计算出基本事件数,根据古典概型概率公式求其概率。(3)属几何概型概率,数形结合需画出图像分析。
试题解析:解:(1)依题意,由 ,解得
,解得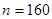 2分
2分
(2)记事件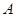 为“
为“ 和
和 至少有一人上台抽奖”, 3分
至少有一人上台抽奖”, 3分
从高二代表队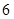 人中抽取
人中抽取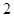 人上台抽奖的所有基本事件列举如下:
人上台抽奖的所有基本事件列举如下: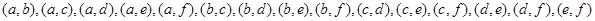 共15种可能, 5分
共15种可能, 5分
其中事件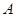 包含的基本事件有9种 6分
包含的基本事件有9种 6分
所以 7分
7分
(3)记事件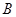 为“该代表中奖”如图,
为“该代表中奖”如图,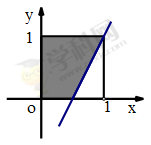
 所表示的平面区域是以
所表示的平面区域是以 为边的正方形,而中奖所表示的平面区域为阴影部分 9分
为边的正方形,而中奖所表示的平面区域为阴影部分 9分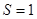 ,阴影部分面积
,阴影部分面积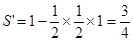 11分
11分
所以该代表中奖的概率为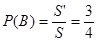 12分
12分
考点:1分层抽样;2古典概型概率;3几何概型概率;4二元一次不等式表示平面区域。

为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 | 频数 | 频率 |
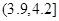 | 3 | 0.06 |
 | 6 | 0.12 |
 | 25 | 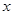 |
 | 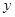 | 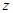 |
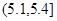 | 2 | 0.04 |
| 合计 | 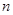 | 1.00 |
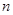 ,
,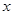 ,
,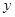 ,
,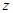 的值
的值(Ⅱ)从样本中视力在
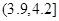 和
和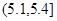 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于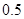 的概率
的概率 

 ,
, ,
, ,现在3名工人独立地从中任意一个项目参与建设.
,现在3名工人独立地从中任意一个项目参与建设. ,参加第五项不合格的概率为
,参加第五项不合格的概率为 .
.