题目内容
已知f(x)=sin(x+θ)+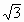 cos(x-θ)为偶函数,求θ的值.
cos(x-θ)为偶函数,求θ的值.
答案:
解析:
解析:
|
解 由条件得f(-x)=f(x),即sin(-x+θ)+ |

练习册系列答案
相关题目
 cos(-x-θ)=sin(x+θ)+
cos(-x-θ)=sin(x+θ)+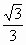 ,∴θ=kπ-
,∴θ=kπ-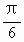 (k∈Z).
(k∈Z). ),g(x)=cos(x-
),g(x)=cos(x- (ω>0),f
(ω>0),f =f
=f ,且f(x)在区间
,且f(x)在区间 上有最小值,无最大值,则ω=________.
上有最小值,无最大值,则ω=________. ),g(x)=cos(x-
),g(x)=cos(x-
 ,0)成中心对称 D.函数y=f(x)g(x)是奇函数
,0)成中心对称 D.函数y=f(x)g(x)是奇函数