题目内容
 选修4-1:几何证明选讲
选修4-1:几何证明选讲如图,从圆O外一点P引圆O的切线PA和割线PBC.
(1)求证:PA2=PB•PC.
(2)已知PA=2
| 2 |
| 3 |
分析:(1)连接AC,AB.由于PA是⊙O的切线,利用弦切角定理可得∠PAB=∠PCA,又∠P公用,可得△PCA∽△PBA.利用相似三角形的性质即可得出;
(2)利用(1)可得BC,过点O作OD⊥BC,垂足为D,连接OB,利用垂径定理可得BD=DC=1.再利用勾股定理可得OB.
(2)利用(1)可得BC,过点O作OD⊥BC,垂足为D,连接OB,利用垂径定理可得BD=DC=1.再利用勾股定理可得OB.
解答:(1)证明:如图所示,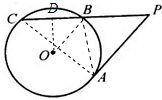
连接AC,AB.∵PA是⊙O的切线,∴∠PAB=∠PCA,又∠P为公共角.
∴△PCA∽△PBA.∴
=
,即PA2=PB•PC.
(2)由PA2=PB•PC,得(2
)2=4PB,解得PB=2.∴BC=PC-PB=2.
过点O作OD⊥BC,垂足为D,连接OB,则BD=DC=1.
又圆心O到BC的距离为
,∴OB=
=2.

连接AC,AB.∵PA是⊙O的切线,∴∠PAB=∠PCA,又∠P为公共角.
∴△PCA∽△PBA.∴
| PC |
| PA |
| PA |
| PB |
(2)由PA2=PB•PC,得(2
| 2 |
过点O作OD⊥BC,垂足为D,连接OB,则BD=DC=1.
又圆心O到BC的距离为
| 3 |
| OD2+BD2 |
点评:熟练掌握圆的切线性质、垂径定理、相似三角形的性质、勾股定理等是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲