题目内容
(本小题满分12分)
在平面直角坐标系xOy中,经过点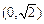 且斜率为k的直线l与椭圆
且斜率为k的直线l与椭圆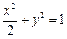 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A、B,是否存在常数k,使得向量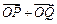 与
与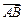 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.
在平面直角坐标系xOy中,经过点
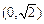 且斜率为k的直线l与椭圆
且斜率为k的直线l与椭圆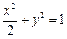 有两个不同的交点P和Q.
有两个不同的交点P和Q. (Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A、B,是否存在常数k,使得向量
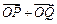 与
与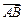 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.(Ⅰ)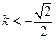 或
或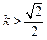 . 即k的取值范围为
. 即k的取值范围为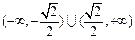
(Ⅱ)解得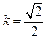 . 由(Ⅰ)知
. 由(Ⅰ)知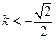 或
或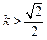 ,故没有符合题意的常数k.
,故没有符合题意的常数k.
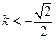 或
或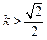 . 即k的取值范围为
. 即k的取值范围为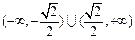
(Ⅱ)解得
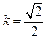 . 由(Ⅰ)知
. 由(Ⅰ)知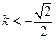 或
或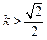 ,故没有符合题意的常数k.
,故没有符合题意的常数k. )解:
(Ⅰ)由已知条件,直线l的方程为
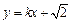 ,
,
代入椭圆方程得
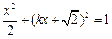 ,
,
整理得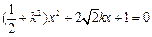 . ① ……3分
. ① ……3分
直线l与椭圆有两个不同的交点P和Q等价于
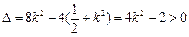 ,
,
解得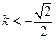 或
或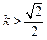 . 即k的取值范围为
. 即k的取值范围为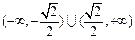 . ……6分
. ……6分
(Ⅱ)设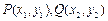 ,则
,则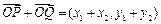 ,
,
由方程①,
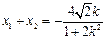 . ②
. ②
又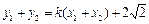 . ③ ……8分
. ③ ……8分
而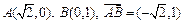 .
.
所以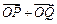 与
与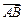 共线等价于
共线等价于
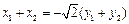 ,
,
将②③代入上式,解得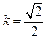 . ……11分
. ……11分
由(Ⅰ)知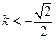 或
或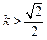 ,故没有符合题意的常数k. ……12分
,故没有符合题意的常数k. ……12分
(Ⅰ)由已知条件,直线l的方程为
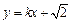 ,
,代入椭圆方程得
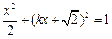 ,
,整理得
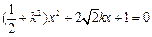 . ① ……3分
. ① ……3分直线l与椭圆有两个不同的交点P和Q等价于
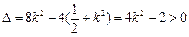 ,
,解得
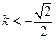 或
或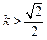 . 即k的取值范围为
. 即k的取值范围为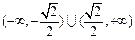 . ……6分
. ……6分(Ⅱ)设
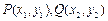 ,则
,则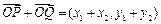 ,
,由方程①,
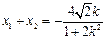 . ②
. ②又
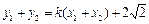 . ③ ……8分
. ③ ……8分而
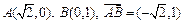 .
.所以
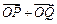 与
与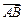 共线等价于
共线等价于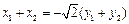 ,
,将②③代入上式,解得
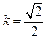 . ……11分
. ……11分由(Ⅰ)知
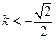 或
或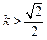 ,故没有符合题意的常数k. ……12分
,故没有符合题意的常数k. ……12分
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: (λ≥2)。
(λ≥2)。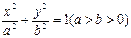 的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=
的左右焦点分别为F1、F2,点P在椭圆C上,且PF1⊥F1F2, |PF1|=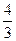 , |PF2|=
, |PF2|=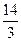 .
. 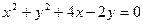 的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。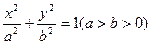 的两个焦点为
的两个焦点为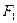 、
、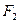 ,点
,点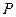 在椭圆C上,且
在椭圆C上,且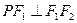 ,
,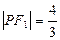 ,
,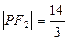 .
. 过圆
过圆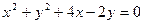 的圆心
的圆心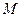 ,交椭圆C于
,交椭圆C于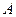 、
、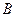 两点,且
两点,且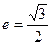 ,且椭圆过点(2,0)。
,且椭圆过点(2,0)。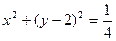 上的点到椭圆C上点的距离的最大值与最小值。
上的点到椭圆C上点的距离的最大值与最小值。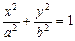 (
( >0)的两个焦点F1,F2,点
>0)的两个焦点F1,F2,点 在椭圆上,则
在椭圆上,则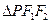 的面积最大值一定是( )
的面积最大值一定是( )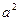 B
B 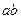 C
C 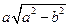 D
D 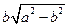
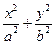 =1(a>b>0)的一个焦点和短轴端点的直线与原点的距离为
=1(a>b>0)的一个焦点和短轴端点的直线与原点的距离为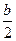 ,则该椭圆的离心率为
,则该椭圆的离心率为 轴上,若焦距为4,则m等于 ( )
轴上,若焦距为4,则m等于 ( )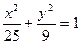 上任一点,F1、F2为椭圆的两焦点,若
上任一点,F1、F2为椭圆的两焦点,若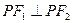 则
则