题目内容
若向量 满足
满足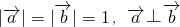 且
且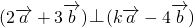 ,则实数k的值为
,则实数k的值为
- A.-6
- B.6
- C.3
- D.-3
B
分析:由题意可得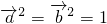 ,
, =0,再由
=0,再由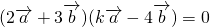 解方程求得实数k的值.
解方程求得实数k的值.
解答:∵向量 满足
满足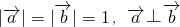 ,且
,且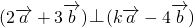 ,
,
可得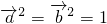 ,
, =0,且
=0,且 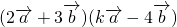 =0,
=0,
故有 2k +(3k-8)
+(3k-8) -12
-12  =0,即 2k-12=0,
=0,即 2k-12=0,
∴k=6,
故选B.
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,属于基础题.
分析:由题意可得
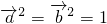 ,
, =0,再由
=0,再由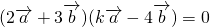 解方程求得实数k的值.
解方程求得实数k的值.解答:∵向量
 满足
满足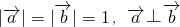 ,且
,且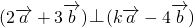 ,
,可得
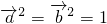 ,
, =0,且
=0,且 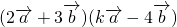 =0,
=0,故有 2k
 +(3k-8)
+(3k-8) -12
-12  =0,即 2k-12=0,
=0,即 2k-12=0,∴k=6,
故选B.
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,属于基础题.

练习册系列答案
相关题目
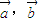 满足
满足 且
且 ,则实数k的值为( )
,则实数k的值为( )