Question

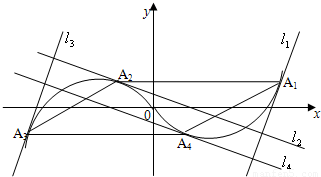
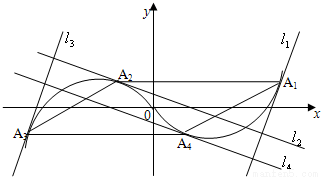
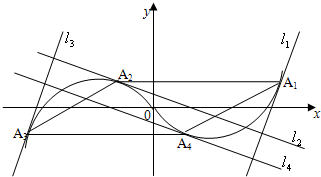如图，在函数y=x³-x的图象上取4个点A_i（x_i，y_i），过点A_i作切线l_i（i=1，2，3，4），如果l₁∥l₃，且l₁，l₂，l₃，l₄围成的图形是矩形记为M．
（1）证明四边形A₁A₂A₃A₄是平行四边形；
（2）问矩形M的短边与长边的比是否有最大值，若有，求l₁与l₂的斜率，若没有，请证明．

Answer 1

分析：（1）先设直线l_i的斜率为k_i（i=1，2，3，4），利用导数的几何意义得出切线的斜率，由题意证出A₁与A₃，A₂与A₄都关于原点对称，从而得出故四边形A₁A₂A₃A₄是平行四边形；
（2）设l₁与l₃的距离为d1=

4| x 3 1 |

1+ k 2 1

，l₂与l₄的距离为d2=

4| x 3 2 |

1+ k 2 2

列出矩形M的短边与长边的比，令g(x)=

(x-1)3

x(x+1)3

（x＞1）利用导数工具研究其单调性和最值，从而得出矩形M的短边与长边的比有最大值及相应的l₁与l₂的斜率．

解答：解：（1）设直线l_i的斜率为k_i（i=1，2，3，4），
由y′=3x²-1，得k_i=3x_i²-（12分）
由题意k₁=k₃，k₂=k₄，又点A₁A₂A₃A₄不重合，故x₁=-x₃，x₂=-x₄，
从而y₁=-y₃，y₂=-y₄，-（5分）
因此A₁与A₃，A₂与A₄都关于原点对称，
故四边形A₁A₂A₃A₄是平行四边形；（7分）
（2）有最大值；      （9分）
设k₁＞0，k₂＜0l_i：y-y_i=k_i（x-x_i），即y-k_ix+2x_i³=0，且k₁k₂=-1
设l₁与l₃的距离为d1=

4| x 3 1 |

1+ k 2 1

，l₂与l₄的距离为d2=

4| x 3 2 |

1+ k 2 2

d 2 2

d 1 1

=

x 6 2

x 6 1

•

1+ k 2 1

1+ k 2 2

=(

k2+1

k1+1

)3

1+ k 2 1

1+ k 2 2

=

1

k1

(

k1-1

k1+1

)3（k＞1）（11分）
令g(x)=

(x-1)3

x(x+1)3

（x＞1）g′(x)=-

(x-1)2(x2-6x-1)

x2(x+1)4

=

[x-(3+ 10 )][x-(3- 10 )](x-1)2

x2(x+1)4

，
当1＜x＜3+

10

时为增函数，
当x＞3+

10

时为减函数，
故当x=3+

10

，gmax(x)=

(2+ 10 )3

(3+ 10 )(4+ 10 )3

（14分）
因为 

(2+ 10 )3

(3+ 10 )(4+ 10 )3

＜1，
因此矩形M的短边与长边的比有最大值，l₁与l₂的斜率分别为3+

10

和3-

10

，（16分）

点评：本小题主要考查两条平行直线间的距离、利用导数研究曲线上某点切线方程、利用导数研究函数的单调性等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．